题目内容
15.已知圆锥的侧面积为6πcm2,侧面展开图的圆心角为60°,则该圆锥的母线长( )| A. | 36cm | B. | 18cm | C. | 6cm | D. | 3cm |
分析 S扇形=$\frac{nπ{r}^{2}}{360}$,把相应数值代入即可.
解答 解:设母线长为r,圆锥的侧面展开后是扇形,侧面积S=$\frac{60π{r}^{2}}{360}$=6π,
∴r=6cm,
故选C.
点评 本题考查了圆锥的计算,利用了扇形的面积公式求解,解题的关键是牢记圆锥的有关公式,难度不大.

练习册系列答案
相关题目
4.关于x,y的方程组$\left\{\begin{array}{l}x+py=0\\ x+y=3\end{array}\right.$的解是$\left\{\begin{array}{l}x=1\\ y=▲\end{array}$,其中y的值被盖住了,不过仍能求出p,则p的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
5.某超市设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“5元”、“10元”、“20元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回),并根据两个小球所标总金额换取等值的购物券.某顾客刚好消费200元,则该顾客所获得购物券的金额不低于20元的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
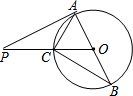 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于C,连结BC、AC,若∠PAC=30°,AC=4,则BC=4$\sqrt{3}$.
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于C,连结BC、AC,若∠PAC=30°,AC=4,则BC=4$\sqrt{3}$.