题目内容
18.若|1-a|+|b+2|=0,则a-b2+$\frac{1}{2}$=-2$\frac{1}{2}$.分析 首先根据|1-a|+|b+2|=0,可得1-a=0,b+2=0,据此求出a、b的值各是多少;然后把求出的a、b的值代入a-b2+$\frac{1}{2}$,求出算式的值是多少即可.
解答 解:∵|1-a|+|b+2|=0,
∴1-a=0,b+2=0,
∴a=1,b=-2,
∴a-b2+$\frac{1}{2}$
=1-(-2)2$+\frac{1}{2}$
=1-4$+\frac{1}{2}$
=-2$\frac{1}{2}$.
故答案为:-2$\frac{1}{2}$.
点评 (1)此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.
(2)此题还考查了绝对值的非负性质的应用,要熟练掌握,解答此题的关键是分别求出a、b的值各是多少.

练习册系列答案
相关题目
8. 如图,⊙O的半径为5,直线l是⊙O的切线,A为切点,则点O到直线l的距离是( )
如图,⊙O的半径为5,直线l是⊙O的切线,A为切点,则点O到直线l的距离是( )
 如图,⊙O的半径为5,直线l是⊙O的切线,A为切点,则点O到直线l的距离是( )
如图,⊙O的半径为5,直线l是⊙O的切线,A为切点,则点O到直线l的距离是( )| A. | 2.5 | B. | 3 | C. | 5 | D. | 10 |
9.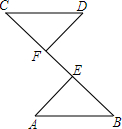 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )| A. | AE=DF | B. | ∠A=∠D | C. | ∠B=∠C | D. | AB=DC |
13.下列说法正确的是( )
| A. | 有最大的负数,没有最小的整数 | |
| B. | 没有最大的有理数,也没有最小的有理数 | |
| C. | 有最大的负数,没有最小的负数 | |
| D. | 有最小的负数,没有最大的正数 |
7.受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
| 到超市的路程(千米) | 运费(元/斤•千米) | |
| 甲养殖场 | 200 | 0.012 |
| 乙养殖场 | 140 | 0.015 |
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
 如图是一个几何体的俯视图,正方形中的数字是该位置上的小立方体数量,请画出从正面和左面看到的图形.
如图是一个几何体的俯视图,正方形中的数字是该位置上的小立方体数量,请画出从正面和左面看到的图形.


