题目内容
9.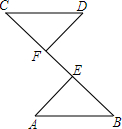 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )| A. | AE=DF | B. | ∠A=∠D | C. | ∠B=∠C | D. | AB=DC |
分析 根据垂直定义求出∠CFD=∠AEB=90°,再根据全等三角形的判定定理推出即可.
解答 解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
$\left\{\begin{array}{l}{AB=CD}\\{BE=CF}\end{array}\right.$,
∴Rt△ABE≌Rt△DCF(HL),
故选D.
点评 本题考查了全等三角形的判定定理的应用,能灵活运用全等三角形的判定定理进行推理是解此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.以下描述中,能确定具体位置的是( )
| A. | 万达电影院2排 | B. | 距薛城高铁站2千米 | ||
| C. | 北偏东30℃ | D. | 东经106℃,北纬31℃ |
17.某县一天中午的温度是15℃,夜间九点下降了17℃,则这天夜间九点的温度是( )
| A. | -2℃ | B. | 8℃ | C. | 12℃ | D. | 18℃ |
4.如图,如果在正方形中画1条纵线和1条横线,便把正方形分成4部分(如图①);如果在正方形中画2条纵线和2条横线,便把正方形分成9部分(如图②);如果在正方形中画3条纵线和3条横线,便把正方形分成16部分(如图③);…,如果在正方形中画9条纵线和9条横线,便把正方形分成( )部分.
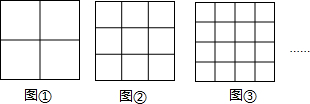

| A. | 72 | B. | 81 | C. | 100 | D. | 121 |
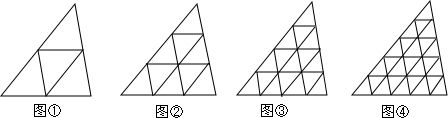
1.如图①,我们知道顺次连接三角形的三边中的(把三边二等分,此时等分数为2)可以吧原三角形分成4分形状与大小相同的小三角形,如果把三条边分别3等分(此时等分数为3),按图②方式将等分点连起来,可以看到整个三角形被分成了9个形状与大小相同的小三角形,…我们来研究这些形状与大小相同的小三角形个数a、顶点数b、边数c与等分数n之间的关系.
(1)如果把三角形的各边分别4等分、5等分,并按上述的方法连接(如图③、图④所示),请将图③、图④中的小三角形个数,顶点数,边数填入上述表格中;
(2)观察上述,如果把三角形的各边分别n等分(此时等分数为n),并按上述的方法连接,形状与大小相同的小三角形个数a,顶点数b,边数c都与等分数n存在一定的关系,请用含n的代数式分别表示出来;
(3)当n=10时,分别求出小三角形个数a、顶点数b、边数c的值.
| 等分数n | 小三角形个数a | 顶点数b | 边数c |
| 2 | 4 | 6 | 9 |
| 3 | 9 | 10 | 18 |
| 4 | 16 | 15 | 30 |
| 5 | 25 | 21 | 45 |
| … | … | … | … |
(2)观察上述,如果把三角形的各边分别n等分(此时等分数为n),并按上述的方法连接,形状与大小相同的小三角形个数a,顶点数b,边数c都与等分数n存在一定的关系,请用含n的代数式分别表示出来;
(3)当n=10时,分别求出小三角形个数a、顶点数b、边数c的值.

 如图所示的圆柱体中底面圆的半径是$\frac{3}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是3$\sqrt{2}$(结果保留根号).
如图所示的圆柱体中底面圆的半径是$\frac{3}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是3$\sqrt{2}$(结果保留根号).