题目内容
14.(1)3$\sqrt{3}-\frac{1}{3}\sqrt{3}+2\sqrt{3}-\frac{4}{3}\sqrt{3}$+1;(2)$\sqrt{5}×\sqrt{2}÷3\sqrt{5}×\frac{{\sqrt{2}}}{2}$;
(3)${9^{\frac{1}{2}}}+{({\frac{1}{2}})^{-3}}+\sqrt{{{({-2})}^2}}$;
(4)${({4-\sqrt{5}})^2}-{({4+\sqrt{5}})^2}$;
(5)${({{{10}^{\frac{1}{2}}}-{2^{\frac{1}{2}}}})^{\frac{1}{3}}}{({{{10}^{\frac{1}{2}}}+{2^{\frac{1}{2}}}})^{\frac{1}{3}}}$;
(6)$2\sqrt{2}+\frac{{\sqrt{5}}}{2}-10\sqrt{0.04}$(精确到0. 01);
(7)${[{{{(2-\sqrt{5})}^2}}]}^{\frac{1}{2}}+{({\sqrt{3}-\sqrt{5}})^0}+{({\frac{1}{27}})^{-\frac{1}{3}}}+{({2\frac{1}{4}})^{\frac{1}{2}}}$.
分析 (1)原式合并同类二次根式即可得到结果;
(2)原式利用二次根式乘除法则计算即可得到结果;
(3)原式利用算术平方根,负整数指数幂法则以及二次根式性质计算即可得到结果;
(4)原式利用完全平方公式计算即可得到结果;
(5)原式逆用积的乘方运算法则变形,再利用平方差公式及完全平方公式计算即可得到结果;
(6)原式取其近似值即可得到结果;
(7)原式利用零指数幂、负整数指数幂法则,以及算术平方根定义计算即可得到结果.
解答 解:(1)原式=$\frac{10}{3}$$\sqrt{3}$;
(2)原式=$\frac{\sqrt{5}×\sqrt{2}}{3\sqrt{5}}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{3}$;
(3)原式=3+8+2=13;
(4)原式=16+5-8$\sqrt{5}$-16-8$\sqrt{5}$-5=-16$\sqrt{5}$;
(5)原式=[($\sqrt{10}$-$\sqrt{2}$)($\sqrt{10}$+$\sqrt{2}$)]${\;}^{\frac{1}{3}}$=$\root{3}{8}$=2;
(6)原式=2$\sqrt{2}$+$\frac{\sqrt{5}}{2}$-2≈1.95;
(7)2-$\sqrt{5}$+1+3+$\frac{3}{2}$=7$\frac{1}{2}$-$\sqrt{5}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
2.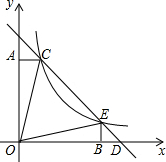 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )| A. | ①②③ | B. | ①②③④ | C. | ②③④⑤ | D. | ①②⑤ |
3.如果两条直线被第三条直线所截,那么一组内错角的平分线( )
| A. | 互相垂直 | B. | 互相平行 | C. | 互相重合 | D. | 不能确定 |