题目内容
8.某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
分析 (1)根据某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元,可以列出相应的分式方程,然后解分式方程即可解答本题;
(2)根据(1)中用电每千米的费用和本问中的信息可以列出相应的不等式,解不等式即可解答本题.
解答 解:(1)设每行驶1千米纯用电的费用为x元,
$\frac{76}{x+0.5}$=$\frac{26}{x}$
解得,x=0.26
经检验,x=0.26是原分式方程的解,
即每行驶1千米纯用电的费用为0.26元;
(2)从A地到B地油电混合行驶,用电行驶y千米,
0.26y+($\frac{26}{0.26}$-y)×(0.26+0.50)≤39
解得,y≥74,
即至少用电行驶74千米.
点评 本题考查分式方程的应用、一元一次不等式的应用,解题的关键是明确题意,列出相应的分式方程与不等式,注意分式方程在最后要检验.

练习册系列答案
相关题目
16.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个记下颜色,再把它放回口袋中,不断重复,如表是活动进行中的一组数据统计:
(1)请估计:当n很大时,摸到白球的频率将会接近0.60;
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑球有8个,白球有12个.
| 摸球的次数m | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数n | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑球有8个,白球有12个.
3.某地一天的最高气温是8℃,最低气温是-2℃,则该地这天的温差是( )
| A. | 10℃ | B. | -10℃ | C. | 6℃ | D. | -6℃ |
13.为了了解某班同学一周的课外阅读量,任选班上15名同学进行调查,统计如表,则下列说法错误的是( )
| 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数(单位:人) | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是2 | D. | 极差是2 |
17.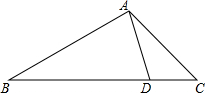 如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
 如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )| A. | 15 | B. | 10 | C. | $\frac{15}{2}$ | D. | 5 |
 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示)
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示)