题目内容
16.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个记下颜色,再把它放回口袋中,不断重复,如表是活动进行中的一组数据统计:| 摸球的次数m | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数n | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑球有8个,白球有12个.
分析 (1)根据表格中数据估计白球的频率即可;
(2)利用频率估计概率得出答案即可;
(3)根据黑、白两种颜色的球共20个,以及摸到白球的概率求出小球个数即可.
解答 解;(1)根据表格中数据的第六行摸到白球的频率,可知当n很大时,摸到白球的频率将会接近0.60;
(2)由(1)知,当摸球的次数n很大,根据频率与概率的关系,摸到白球的实验概率近似等于摸到白球的频率,所以摸到白球的概率约为0.60,摸到黑球的概率是0.40;
(3)盒子中白球的个数约为20×0.6=12(个),
则黑球个数为:20-12=8(个);
故答案为:0.60;0.60;0.40;8;12.
点评 此题主要考查了利用频率估计概率,根据表格估计出得到白球的概率是解题关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
7. 下面所给几何体的俯视图是( )
下面所给几何体的俯视图是( )
 下面所给几何体的俯视图是( )
下面所给几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
11.某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )
| A. | 103块 | B. | 104块 | C. | 105块 | D. | 106块 |
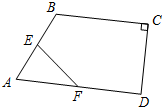 已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=$\sqrt{13}$.
已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=$\sqrt{13}$. 如图,直线y=-$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$交于A、B两点,且点A的坐标为(-6,m),则双曲线y=$\frac{k}{x}$的解析式为y=-$\frac{12}{x}$.
如图,直线y=-$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$交于A、B两点,且点A的坐标为(-6,m),则双曲线y=$\frac{k}{x}$的解析式为y=-$\frac{12}{x}$. 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.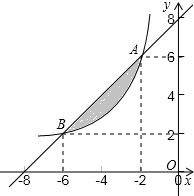 如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.
如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.