题目内容
18.已知关于x的方程$\frac{3x}{{x}^{2}-1}$+$\frac{{x}^{2}-1}{x}$=$\frac{5}{2}$,如果设$\frac{x}{{x}^{2}-1}$=y,那么原方程化为关于y的方程是3y+$\frac{1}{y}$=$\frac{5}{2}$.分析 先根据$\frac{x}{{x}^{2}-1}$=y得到$\frac{{x}^{2}-1}{x}=\frac{1}{y}$,再代入原方程进行换元即可.
解答 解:由$\frac{x}{{x}^{2}-1}$=y,可得$\frac{{x}^{2}-1}{x}=\frac{1}{y}$
∴原方程化为3y+$\frac{1}{y}$=$\frac{5}{2}$
故答案为:3y+$\frac{1}{y}$=$\frac{5}{2}$
点评 本题主要考查了换元法解分式方程,换元的实质是转化,将复杂问题简单化.常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,用一个字母来代替它可以简化问题,有时候要通过变形才能换元.

练习册系列答案
相关题目
9.下列事件中,是确定事件的是( )
| A. | 打开电视,它正在播郑州新闻 | B. | 抛掷一枚一元的硬币,正面朝上 | ||
| C. | 367人中有两人的生日相同 | D. | 打雷后会下雨 |
3.已知弹簧在一定限度内,它的长度y(厘米)与所挂重物质量x(千克)是一次函数关系.表中记录的是两次挂不同重量重物的质量(在弹性限度内)与相对应的弹簧长度.
求不挂重物时弹簧的长度.
| 所挂重物质量x(千克) | 2.5 | 5 |
| 弹簧长度y(厘米) | 7.5 | 9 |
7. 下面所给几何体的俯视图是( )
下面所给几何体的俯视图是( )
 下面所给几何体的俯视图是( )
下面所给几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
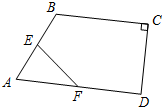 已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=$\sqrt{13}$.
已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=$\sqrt{13}$.