题目内容
怎样平移函数y=-
x2的图象后就可以得到函数y=-
x2-2x+1的图象?
| 1 |
| 2 |
| 1 |
| 2 |
考点:二次函数图象与几何变换
专题:
分析:按照“左加右减,上加下减”的规律求则可.
解答:解:函数y=-
x2图象向左平移2个单位,得抛物线y=-
(x+2)2,再向上平移3个单位可得到抛物线y=-
(x+2)2+3=-
x2-2x+1.
故将函数y=-
x2的图象先向左平移2个单位,再向上平移3个单位可以得到函数y=-
x2-2x+1的图象.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故将函数y=-
| 1 |
| 2 |
| 1 |
| 2 |
点评:考查了抛物线的平移以及抛物线解析式的变化规律:左加右减,上加下减.

练习册系列答案
相关题目
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(0,-3),且对称轴为x=2,则这条抛物线的顶点坐标为( )
| A、(2,3) |
| B、(2,1) |
| C、(-2,1) |
| D、(2,-1) |
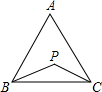 如图,在△ABC中,AB=AC,∠A=50°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )
如图,在△ABC中,AB=AC,∠A=50°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )| A、100° | B、115° |
| C、130° | D、65° |
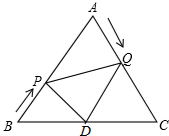 已知△ABC是边长为6cm的等边三角形,动点P、Q同时从B、A两点出发,分别沿BA、AC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
已知△ABC是边长为6cm的等边三角形,动点P、Q同时从B、A两点出发,分别沿BA、AC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题: