题目内容
9.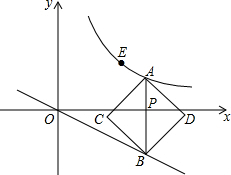 如图,在直角坐标系中,已知点E(3,2)在双曲线y=$\frac{k}{x}$(x>0)上.过动点P(t,0)作x轴的垂线分别与该双曲线和直线y=-$\frac{1}{2}$x交于A、B两点,以线段AB为对角线作正方形ADBC,当正方形ADBC的边(不包括正方形顶点)经过点E时,则t的值为2或$\frac{2}{3}$.
如图,在直角坐标系中,已知点E(3,2)在双曲线y=$\frac{k}{x}$(x>0)上.过动点P(t,0)作x轴的垂线分别与该双曲线和直线y=-$\frac{1}{2}$x交于A、B两点,以线段AB为对角线作正方形ADBC,当正方形ADBC的边(不包括正方形顶点)经过点E时,则t的值为2或$\frac{2}{3}$.
分析 存在两种情况:①当AD经过点E时,先求出双曲线的解析式,再求出直线AD的解析式,把A(t,$\frac{6}{t}$)代入一次函数解析式即可求出t的值;
②当BD经过点E时,先求出直线BD的解析式,再把B(t,-$\frac{1}{2}$t)代入直线BD的解析式即可求出t的值.
解答 解:存在两种情况:①当AD经过点E时,如图1所示: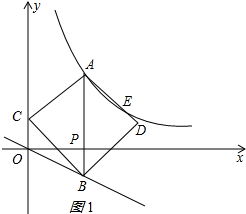 ∵点E(3,2)在双曲线y=$\frac{k}{x}$(x>0)上,
∵点E(3,2)在双曲线y=$\frac{k}{x}$(x>0)上,
∴k=3×2=6,
∴双曲线解析式为:y=$\frac{6}{x}$,
∵四边形ADBC是正方形,
∴∠DAB=$\frac{1}{2}$∠DAC=45°,
∵AB⊥x轴,
∴设直线AD的解析式为y=-x+b,
把点E(3,2)代入得:b=5,
∴直线AD的解析式为:y=-x+5,
设A(t,$\frac{6}{t}$),代入y=-x+5得:-t+5=$\frac{6}{t}$,
解得:t=2,或t=3(不合题意,舍去),
∴t=2;
②当BD经过点E时,如图2所示: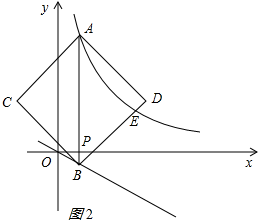 ∵BD⊥AD,
∵BD⊥AD,
∴设直线BD的解析式为:y=x+c,
把点E(3,2)代入得:c=-1,
∴直线BD的解析式为:y=x-1,
设B(t,-$\frac{1}{2}$t),代入y=x-1得:
-$\frac{1}{2}$t=t-1,
解得:t=$\frac{2}{3}$;
综上所述:当正方形ADBC的边(不包括正方形顶点)经过点E时,t的值为:2或$\frac{2}{3}$;
故答案为:2或$\frac{2}{3}$.
点评 本题是反比例函数综合题目,考查了用待定系数法求反比例函数和一次函数的解析式、坐标与图形性质、正方形的性质等知识;本题难度较大,综合性强,需要进行分类讨论,求出相关直线的解析式才能得出结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. 如图,表示$\sqrt{7}$的点在数轴上表示时,所在哪两个字母之间( )
如图,表示$\sqrt{7}$的点在数轴上表示时,所在哪两个字母之间( )
 如图,表示$\sqrt{7}$的点在数轴上表示时,所在哪两个字母之间( )
如图,表示$\sqrt{7}$的点在数轴上表示时,所在哪两个字母之间( )| A. | C与D | B. | A与B | C. | A与C | D. | B与C |
14.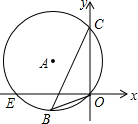 如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
 如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{16}$ |
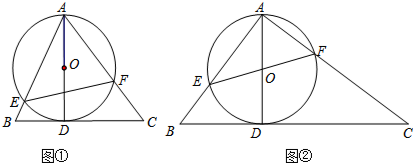
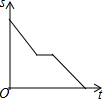
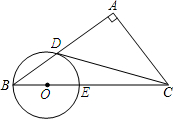 在Rt△ABC中,∠A=90°,点O在BC上,以点O为圆心,OB长为半径的圆与AB、BC分别交于点D、E,且∠ACD=∠B.
在Rt△ABC中,∠A=90°,点O在BC上,以点O为圆心,OB长为半径的圆与AB、BC分别交于点D、E,且∠ACD=∠B.