题目内容
7.已知抛物线y=x2-x-2经过点(m,5),则m2-m+2的值为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 直接利用二次函数图象上点的坐标性质得出关于m的等式,进而得出答案.
解答 解:∵抛物线y=x2-x-2经过点(m,5),
∴5=m2-m-2,
故m2-m=7,
∴m2-m+2=9.
故选:C.
点评 此题主要考查了二次函数图象上点的坐标特征,正确得出m2-m的值是解题关键.

练习册系列答案
相关题目
17.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:
那么这9名学生所得分数的众数和中位数分别是( )
| 人数(人) | 1 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
15.如图所示的几何体,其俯视图是( )
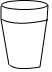

| A. | 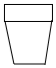 | B. | 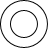 | C. |  | D. |  |
12.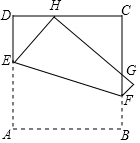 如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
 如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | ||
| C. | $\frac{\sqrt{5}-1}{2}$ | D. | 随H点位置的变化而变化 |
17.计算$\frac{a}{a+1}+\frac{1}{a+1}$的结果为( )
| A. | 1 | B. | a | C. | a+1 | D. | $\frac{1}{a+1}$ |
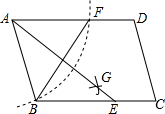 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )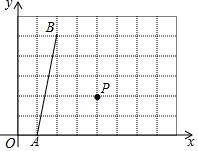 如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为(7,4)或(6,5)或(1,4).
如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为(7,4)或(6,5)或(1,4).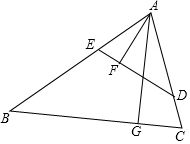 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.