题目内容
19.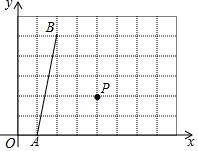 如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为(7,4)或(6,5)或(1,4).
如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为(7,4)或(6,5)或(1,4).
分析 由勾股定理求出PA=PB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,由点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,得出PC=PA=PB=$\sqrt{13}$,即可得出点C的坐标.
解答 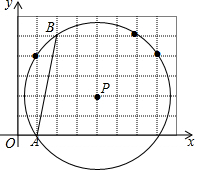 解:如图,
解:如图,
∵点A、B、P的坐标分别为(1,0),(2,5),(4,2).
∴PA=PB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∵点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,
∴PC=PA=PB=$\sqrt{13}$=$\sqrt{{2}^{2}+{3}^{2}}$,
则点C的坐标为 (7,4)或(6,5)或(1,4);
故答案为:(7,4)或(6,5)或(1,4).
点评 本题考查了三角形的外接圆、坐标与图形性质、勾股定理;熟练掌握勾股定理是解决问题的关键.

练习册系列答案
相关题目
9.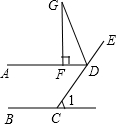 如图,直线AD∥BC,点C、D、E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )
如图,直线AD∥BC,点C、D、E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )
 如图,直线AD∥BC,点C、D、E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )
如图,直线AD∥BC,点C、D、E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )| A. | 50° | B. | 30° | C. | 25° | D. | 15° |
10.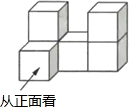 由6个大小相同的正方体搭成的几何体如图所示,比较它的正视图、左视图和俯视图的面积,则( )
由6个大小相同的正方体搭成的几何体如图所示,比较它的正视图、左视图和俯视图的面积,则( )
 由6个大小相同的正方体搭成的几何体如图所示,比较它的正视图、左视图和俯视图的面积,则( )
由6个大小相同的正方体搭成的几何体如图所示,比较它的正视图、左视图和俯视图的面积,则( )| A. | 三个视图的面积一样大 | B. | 主视图的面积最小 | ||
| C. | 左视图的面积最小 | D. | 俯视图的面积最小 |
7.已知抛物线y=x2-x-2经过点(m,5),则m2-m+2的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
8.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a的值为( )


| A. | 23 | B. | 75 | C. | 77 | D. | 139 |
9.用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.
设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
| 一次复印页数(页) | 5 | 10 | 20 | 30 | … |
| 甲复印店收费(元) | 0.5 | 1 | 2 | 3 | … |
| 乙复印店收费(元) | 0.6 | 1.2 | 2.4 | 3.3 | … |
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.
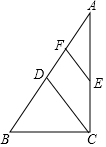 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF=2.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF=2.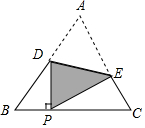 如图,把等边△A BC沿着D E折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4cm,则EC=(2+2$\sqrt{3}$)cm.
如图,把等边△A BC沿着D E折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4cm,则EC=(2+2$\sqrt{3}$)cm.