题目内容

2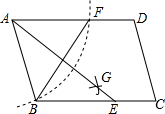．如图，在?ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为（　　）
A．10B．8C．6D．4

分析 先求AB=BE=5，利用勾股定理求AH=EH=4，得AE=8．

解答 解：∵AG平分∠BAD，
∴∠BAG=∠DAG，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠AEB=∠DAG，
∴∠BAG=∠AEB，
∴AB=BE=5，
由作图可知：AB=AF，
∠BAE=∠FAE，
∴BH=FH=3，BF⊥AE，
由勾股定理得：AH=EH=4，
∴AE=8，
故选B．

点评 本题考查了平行四边形的性质、勾股定理、角平分线的作法和定义、等腰三角形三线合一的性质，熟练掌握平行加角平分线可得等腰三角形，属于常考题型．

练习册系列答案
相关题目
12．如图所示是五个棱长为“1”的小立方块组成的一个几何体，下列选项中不是三视图其中之一的是（　　）
A．B．C．D．
13．某种股票原价格为a元，连续两天上涨，每次涨幅10%，则该股票两天后的价格为（　　）
A．1.21a元B．1.1a元C．1.2a元D．（0.2+a） 元
10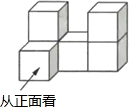．由6个大小相同的正方体搭成的几何体如图所示，比较它的正视图、左视图和俯视图的面积，则（　　）
A．三个视图的面积一样大B．主视图的面积最小
C．左视图的面积最小D．俯视图的面积最小
17．探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用图1得到结论：P1P2=$\sqrt{{{（{{x_2}-{x_1}}）}^2}+{{（{{y_2}-{y_1}}）}^2}}$他还利用图2证明了线段P1P2的中点P（x，y）P的坐标公式：x=$\frac{{{x_1}+{x_2}}}{2}$，y=$\frac{{{y_1}+{y_2}}}{2}$．

（1）请你帮小明写出中点坐标公式的证明过程；
运用：（2）①已知点M（2，-1），N（-3，5），则线段MN长度为$\sqrt{61}$；
②直接写出以点A（2，2），B（-2，0），C（3，-1），D为顶点的平行四边形顶点D的坐标：（-3，3）或（7，1）或（-1，-3）；
拓展：（3）如图3，点P（2，n）在函数y=$\frac{4}{3}$x（x≥0）的图象OL与x轴正半轴夹角的平分线上，请在OL、x轴上分别找出点E、F，使△PEF的周长最小，简要叙述作图方法，并求出周长的最小值．
7．已知抛物线y=x2-x-2经过点（m，5），则m2-m+2的值为（　　）
A．7B．8C．9D．10
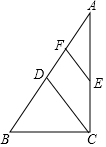14．如图，在Rt△ABC中，∠ACB=90°，点D，E分别是AB，AC的中点，点F是AD的中点．若AB=8，则EF=2．
11．我们定义：如图1，在△ABC中，把AB点绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC'，连接B'C'．当α+β=180°时，我们称△A'B'C'是△ABC的“旋补三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．
特例感知：
（1）在图2，图3中，△AB'C'是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．
①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD=$\frac{1}{2}$BC；
②如图3，当∠BAC=90°，BC=8时，则AD长为4．
猜想论证：
（2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．
拓展应用
（3）如图4，在四边形ABCD，∠C=90°，∠D=150°，BC=12，CD=2$\sqrt{3}$，DA=6．在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，给予证明，并求△PAB的“旋补中线”长；若不存在，说明理由．
12．计算（-3）+5的结果等于（　　）
A．2B．-2C．8D．-8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网