题目内容
16.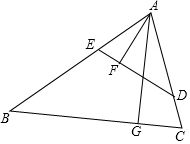 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求$\frac{AF}{AG}$的值.
分析 (1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,从而可证明∠AED=∠ACB,进而可证明△ADE∽△ABC;
(2)△ADE∽△ABC,$\frac{AD}{AB}=\frac{AE}{AC}$,又易证△EAF∽△CAG,所以$\frac{AF}{AG}=\frac{AE}{AC}$,从而可知$\frac{AF}{AG}=\frac{AD}{AB}$.
解答 解:(1)∵AG⊥BC,AF⊥DE,
∴∠AFE=∠AGC=90°,
∵∠EAF=∠GAC,
∴∠AED=∠ACB,
∵∠EAD=∠BAC,
∴△ADE∽△ABC,
(2)由(1)可知:△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{AE}{AC}$=$\frac{3}{5}$
由(1)可知:∠AFE=∠AGC=90°,
∴∠EAF=∠GAC,
∴△EAF∽△CAG,
∴$\frac{AF}{AG}=\frac{AE}{AC}$,
∴$\frac{AF}{AG}$=$\frac{3}{5}$
点评 本题考查相似三角形的判定,解题的关键是熟练运用相似三角形的判定,本题属于中等题型.

练习册系列答案
相关题目
7.已知抛物线y=x2-x-2经过点(m,5),则m2-m+2的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
1.在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为( )
| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
8.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a的值为( )


| A. | 23 | B. | 75 | C. | 77 | D. | 139 |
6.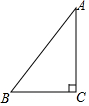 如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
 如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
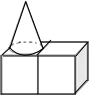 如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,画出实物的三视图.
如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,画出实物的三视图.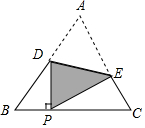 如图,把等边△A BC沿着D E折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4cm,则EC=(2+2$\sqrt{3}$)cm.
如图,把等边△A BC沿着D E折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4cm,则EC=(2+2$\sqrt{3}$)cm.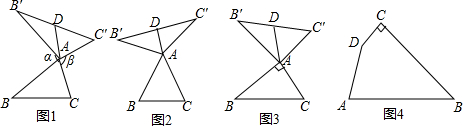
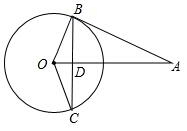 如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=60°.
如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=60°.