题目内容
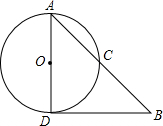 如图,AD为⊙O的直径,DE切⊙O于D,AE交⊙O于C,求证:AD2=AC•AE.
如图,AD为⊙O的直径,DE切⊙O于D,AE交⊙O于C,求证:AD2=AC•AE.考点:切线的性质,相似三角形的判定与性质
专题:证明题
分析:连结CD,如图,先根据圆周角定理,由AD为⊙O的直径得到∠ACD=90°,再根据切线的性质,由DE切⊙O于D得到∠ADE=90°,然后根据相似三角形的判定方法证明Rt△ACD∽Rt△ADE,利用相似的性质得
=
,再利用比例的性质即可得到结论.
| AC |
| AD |
| AD |
| AE |
解答:证明:连结CD,如图,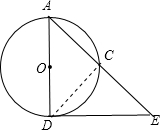
∵AD为⊙O的直径,
∴∠ACD=90°,
∵DE切⊙O于D,
∴AD⊥DE,
∴∠ADE=90°,
∵∠CAD=∠DAE,
∴Rt△ACD∽Rt△ADE,
∴
=
,
∴AD2=AC•AE.

∵AD为⊙O的直径,
∴∠ACD=90°,
∵DE切⊙O于D,
∴AD⊥DE,
∴∠ADE=90°,
∵∠CAD=∠DAE,
∴Rt△ACD∽Rt△ADE,
∴
| AC |
| AD |
| AD |
| AE |
∴AD2=AC•AE.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了相似三角形的判定与性质.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
用一个平面去截正方体,截面形状不可能的是( )
| A、三角形 | B、梯形 |
| C、六边形 | D、七边形 |
如果am=an,那么下列等式不一定成立的是( )
| A、am-3=an-3 | ||||
| B、5+am=5+an | ||||
| C、m=n | ||||
D、-
|
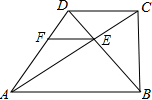 如图,在四边形ABCD中,∠ABC=90°,AD=BD,AC,BD相交于点E,AC⊥BD,垂足为E,过点E作EF∥AB,交AD于点F.
如图,在四边形ABCD中,∠ABC=90°,AD=BD,AC,BD相交于点E,AC⊥BD,垂足为E,过点E作EF∥AB,交AD于点F.