题目内容
在△ABC中,AB=9,AC=40,BC=41,三角形的外心在 上,外接圆半径长为 .
考点:三角形的外接圆与外心,勾股定理的逆定理
专题:
分析:首先利用勾股定理逆定理得出△ABC是直角三角形,进而利用直角三角形外心在斜边的中点上,斜边为其外接圆直径,进而得出答案.
解答:解:∵AB=9,AC=40,BC=41,
则92+402=412,
∴△ABC是直角三角形,
∴三角形的外心在BC边中点上,
外接圆半径长为:
=20.5.
故答案为:BC边中点,20.5.
则92+402=412,
∴△ABC是直角三角形,
∴三角形的外心在BC边中点上,
外接圆半径长为:
| 41 |
| 2 |
故答案为:BC边中点,20.5.
点评:此题主要考查了勾股定理逆定理以及直角三角形的外接圆与外心,正确把握直角三角形的性质是解题关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
用一个平面去截正方体,截面形状不可能的是( )
| A、三角形 | B、梯形 |
| C、六边形 | D、七边形 |
 如图,当太阳光与地面成60°角时,测得直立于地面的玲玲的影长为1m,则玲玲的身高为( )m.
如图,当太阳光与地面成60°角时,测得直立于地面的玲玲的影长为1m,则玲玲的身高为( )m.| A、2 | ||||
B、-
| ||||
C、-
| ||||
D、
|
下列命题中,假命题有( )
①相等的角是对顶角;②两直线平行,内错角相等;③两直角边的平方和等于第三边平方;④如果一个四边形是平行四边形,那么它一定是对称图形;⑤SSA是判定全等三角形的一种方法.
①相等的角是对顶角;②两直线平行,内错角相等;③两直角边的平方和等于第三边平方;④如果一个四边形是平行四边形,那么它一定是对称图形;⑤SSA是判定全等三角形的一种方法.
| A、1个 | B、2个 | C、3个 | D、4个 |
下列运算中错误的是( )
| A、-22=-4 |
| B、2x-x=1 |
| C、-(-5)=5 |
| D、-1-1=-2 |
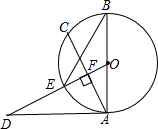 如图所示,⊙O直径AB=10,AD是⊙O的切线,OD⊥弦AC于点F,且交⊙O于点E,有下列结论:
如图所示,⊙O直径AB=10,AD是⊙O的切线,OD⊥弦AC于点F,且交⊙O于点E,有下列结论: