题目内容
某轮渡公司的一艘轮船在烟台与大连之间往返航行.在冬季期间,轮船到大连顶风航行,停留一段时间后(卸货、装货、加注燃料等),返回烟台时顺风航行.若该轮船从烟台出发后所用的时间为x(小时),轮船距烟台的距离为y(千米).则下列各图中,能够反映y与x之间的函数关系的大致图象是( )
A、 |
B、 |
C、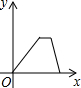 |
D、 |
考点:函数的图象
专题:
分析:分三段考虑:①逆水行驶;②静止不动;③顺水行驶;结合图象判断即可.
解答:解:分三段考虑,
①逆水行驶,y随x的增大而缓慢增大;
②静止不动,y随x的增加,不变;
③顺水行驶,y随x的增减快速减小.
结合图象,可得C选项正确.
故选:C.
①逆水行驶,y随x的增大而缓慢增大;
②静止不动,y随x的增加,不变;
③顺水行驶,y随x的增减快速减小.
结合图象,可得C选项正确.
故选:C.
点评:本题考查了函数的图象,解答本题的关键是仔细审题,将实际与函数图象结合起来,分段看图象.

练习册系列答案
相关题目
 如图,当太阳光与地面成60°角时,测得直立于地面的玲玲的影长为1m,则玲玲的身高为( )m.
如图,当太阳光与地面成60°角时,测得直立于地面的玲玲的影长为1m,则玲玲的身高为( )m.| A、2 | ||||
B、-
| ||||
C、-
| ||||
D、
|
下列命题中,假命题有( )
①相等的角是对顶角;②两直线平行,内错角相等;③两直角边的平方和等于第三边平方;④如果一个四边形是平行四边形,那么它一定是对称图形;⑤SSA是判定全等三角形的一种方法.
①相等的角是对顶角;②两直线平行,内错角相等;③两直角边的平方和等于第三边平方;④如果一个四边形是平行四边形,那么它一定是对称图形;⑤SSA是判定全等三角形的一种方法.
| A、1个 | B、2个 | C、3个 | D、4个 |
如果∠l与∠2互补,若∠2为锐角,则下列表示∠2余角的式子是( )
| A、90°-∠1 |
| B、180°-∠1 |
| C、∠1+90° |
| D、∠1-90° |
如果am=an,那么下列等式不一定成立的是( )
| A、am-3=an-3 | ||||
| B、5+am=5+an | ||||
| C、m=n | ||||
D、-
|
下列图案中,既是中心对称图形,又是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列运算中错误的是( )
| A、-22=-4 |
| B、2x-x=1 |
| C、-(-5)=5 |
| D、-1-1=-2 |