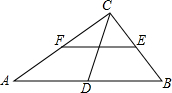如图.在Rt△ABC中.∠ACB=90°.D.E.F分别是AB.BC.CA的中点.若CD=5cm.则EF为( )A．5B．10C．15D．20 题目和参考答案——青夏教育精英家教网—

题目内容

3．

如图，在Rt△ABC中，∠ACB=90°，D，E，F分别是AB，BC，CA的中点，若CD=5cm，则EF为（　　）

A．

B．

C．

D．

分析根据直角三角形斜边上的中线等于斜边的一半求出AB，再根据三角形的中位线平行于第三边并且等于第三边的一半求解即可．

解答解：∵∠ACB=90°，D是AB的中点，
∴AB=2CD=2×5=10cm，
∴E，F分别是BC，CA的中点，
∴EF是△ABC的中位线，
∴EF=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5cm．
故选A．

点评本题考查了直角三角形斜边上的中线等于斜边的一半的性质，三角形的中位线平行于第三边并且等于第三边的一半，熟记性质与定理是解题的关键．

练习册系列答案

相关题目

10．

（1）计算：$\sqrt{8}$-（π-1）⁰-4sin45°；
（2）解不等式x＞$\frac{1}{3}$x-2，并将其解集表示在数轴上．

14．二次函数y=x²+px+q中，由于二次项系数为1＞0，所以在对称轴左侧，y随x增大而减小，从而得到y越大则x越小，在对称轴右侧，y随x增大而减大，从而得到y越大则x也越大，请根据你对这句话的理解，解决下面问题：若关于x的方程x²+px+q+1=0的两个实数根是m、n（m＜n），关于x的方程x²+px+q-5=0的两个实数根是d、e（d＜e），则m、n、d、e的大小关系是（　　）

11．我们把能平分多边形面积的直线称为该多边形的“好线”．小明通过学习知道：
（1）三角形的任意一条中线所在的直线都是该三角形的“好线”
（2）要画出某个平行四边形的“好线”，只要画出任意一条经过该平行四边形中心的一条直线即可（如图1）
根据上面的结论，小明继续探究以下两个问题，请你尝试完成：
（1）画出图2中多边形的三条不同的“好线”（要求：在备用图1、2、3中各画出一条）
（2）如图3，梯形ABCD中，AB=6，CD=2，梯形的一条“好线”过点C与AB交于点E，则AE的长为2．

18．下面是解分式方程的过程，阅读完后请填空：
解方程：$\frac{480}{x}-\frac{600}{2x}$=45．
解：方程两边都乘以2x，得960-600=90x
解这个方程，得x=4．
经检验，x=4是原方程的根．
第一步计算中的2x是：分母x和2x的最简公分母；这个步骤用到的依据是等式的基本性质；
解分式方程与解一元一次方程之间的联系是：解分式方程就是利用等式的基本性质把分式方程转化为一元一次方程来求解．

8．

如图，点A、点B、点C均在⊙O上，若∠B=40°，则∠AOC的度数为（　　）

15．化简：$\frac{x-3}{{x}^{2}-4}$•（1+$\frac{{x}^{2}+x+3}{x-3}$）．

12．

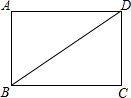如图，BD是矩形ABCD的一条对角线．
（1）作BD的垂直平分线EF，分别交AD，BC于点E，F，垂足为点O（要求用尺规作图，保留作图痕迹，不要求写作法）
（2）在（1）中，连接BE和DF，求证：四边形DEBF是菱形．

13．

如图，直线l₁∥l₂，∠1=55°，则∠2的度数是（　　）

试题分类