题目内容
20.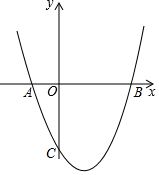 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,-3),A点的坐标为(-1,0).
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,-3),A点的坐标为(-1,0).(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,
求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,直接写出使△QBC为直角三角形的点Q的
坐标.
分析 (1)把A、C两点坐标代入可求得b、c的值,可求得二次函数的解析式;
(2)由抛物线解析式可求得B点坐标,由B、C坐标可求得直线BC解析式,可设出P点坐标,用P点坐标表示出四边形ABPC的面积,根据二次函数的性质可求得其面积的最大值及P点坐标;
(3)由抛物线解析式可求得其对称轴,则可设出Q点的坐标,则可表示出QB2、QC2和BC2,分∠BQC=90°、∠CBQ=90°和∠BCQ=90°三种情况,分别根据勾股定理得到关于Q点坐标的方程,可求得Q点的坐标.
解答 解:
(1)∵A(-1,0),C(0,-3)在y=x2+bx+c上,
∴$\left\{\begin{array}{l}1-b+c=0\\ c=-3\end{array}\right.$,解得$\left\{\begin{array}{l}b=-2\\ c=-3\end{array}\right.$,
∴二次函数的解析式为y=x2-2x-3;
(2)在y=x2-2x-3中,令y=0可得0=x2-2x-3,解得x=3或x=-1,
∴B(3,0),且C(0,-3),
∴经过B、C两点的直线为y=x-3,
设点P的坐标为(x,x2-2x-3),如图,过点P作PD⊥x轴,垂足为D,与直线BC交于点E,则E(x,x-3),
∵S四边形ABPC=S△ABC+S△BCP=$\frac{1}{2}$×4×3+$\frac{1}{2}$(3x-x2)×3=-$\frac{3}{2}$x2+$\frac{9}{2}$x+6=$-\frac{3}{2}{({x-\frac{3}{2}})^2}+\frac{75}{8}$,
∴当$x=\frac{3}{2}$时,四边形ABPC的面积最大,此时P点坐标为($\frac{3}{2}$,-$\frac{15}{4}$),
∴四边形ABPC的最大面积为$\frac{75}{8}$;
(3)∵y=x2-2x-3=(x-1)2-4,
∴对称轴为x=1,
∴可设Q点坐标为(1,t),
∵B(3,0),C(0,-3),
∴BQ2=(1-3)2+t2=t2+4,CQ2=12+(t+3)2=t2+6t+10,BC2=18,
∵△QBC为直角三角形,
∴有∠BQC=90°、∠CBQ=90°和∠BCQ=90°三种情况,
①当∠BQC=90°时,则有BQ2+CQ2=BC2,即t2+4+t2+6t+10=18,解得t=$\frac{-3+\sqrt{17}}{2}$或t=$\frac{-3-\sqrt{17}}{2}$,此时Q点坐标为(1,$\frac{-3+\sqrt{17}}{2}$)或(1,$\frac{-3-\sqrt{17}}{2}$);
②当∠CBQ=90°时,则有BC2+BQ2=CQ2,即t2+4+18=t2+6t+10,解得t=2,此时Q点坐标为(1,2);
③当∠BCQ=90°时,则有BC2+CQ2=BQ2,即18+t2+6t+10=t2+4,解得t=-4,此时Q点坐标为(1,-4);
综上可知Q点的坐标为(1,$\frac{-3+\sqrt{17}}{2}$)或(1,$\frac{-3-\sqrt{17}}{2}$)或(1,2)或(1,-4).
点评 本题为二次函数的综合应用,涉及待定系数法、三角形的面积、二次函数的性质、勾股定理、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中用P点坐标表示出四边形ABPC的面积是解题的关键,在(3)中用Q点坐标分别表示出BQ和CQ的长是解题的关键,注意分类讨论.本题考查知识点较多,综合性较强,难度适中.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 3,4,5 | C. | 6,7,8 | D. | 2,3,4 |
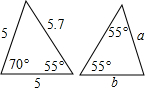 如图所示的两个三角形是全等三角形,根据图中信息,可得a+b的值为( )
如图所示的两个三角形是全等三角形,根据图中信息,可得a+b的值为( )| A. | 5.7 | B. | 10 | C. | 10.7 | D. | 11.7 |
 如图,直线AB、CD相交于点O,OE平分∠BOD.
如图,直线AB、CD相交于点O,OE平分∠BOD.