题目内容
4．
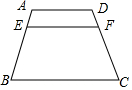在梯形ABCD中，EF∥AD∥BC，要使梯形AEFD∽梯形EBCF，则应满足的条件是（ ）| A． | EF=$\frac{1}{2}$BC | B． | EF2=AD•BC | C． | AE=EB | D． | $\frac{AE}{AB}$=$\frac{AD}{EF}$ |
分析 先根据梯形AEFD∽梯形EBCF，AE与EB是相似梯形的对应边，根据相似多边形的对应边的比值相等，进而得出答案．
解答 解：当梯形AEFD∽梯形EBCF，
∴$\frac{AD}{EF}$=$\frac{EF}{BC}$=$\frac{AE}{EB}$，
∴EF2=AD•BC，
故选：B．
点评 本题考查的是相似多边形的性质，熟知相似多边形的对应边成比例是解答此题的关键．
练习册系列答案
相关题目
14．下列计算正确的是（ ）
| A． | （±$\frac{1}{4}$）2=$\frac{1}{2}$ | B． | ±（$\sqrt{1\frac{9}{16}}$）=±1$\frac{1}{4}$ | C． | -$\sqrt{0.9}$=-0.3 | D． | $\sqrt{1{3}^{2}-{7}^{2}}$=6 |
15．下列说法错误的是（ ）
| A． | 平行四边形的对角相等 | |
| B． | 正方形的对称轴有四条 | |
| C． | 矩形既是中心对称图形又是轴对称图形 | |
| D． | 菱形的对角线相等且互相平分 |
16．若a＜0，b＜0，则下列各式正确的是（ ）
| A． | a-b＜0 | B． | a-b＞0 | C． | a-b=0 | D． | ab＞0 |
13．一元二次方程（x-2）2=1可转化为两个一元一次方程，其中一个一元一次方程是x-2=-1，则另一个一元一次方程是（ ）
| A． | x-2=1 | B． | x+2=1 | C． | x+2=-1 | D． | x-2=-1 |