题目内容
19.数轴上两点之间的距离等于相应两数差的绝对值.①数轴上表示-3和-9的两点之间的距离是6;数轴上表示2和-8的两点之间的距离是10;
②数轴上表示x和-2的两点A和B之间的距离是|x+2|;如果|AB|=4,那么x为2或-6;
③当代数式|x+1|+|x-2|+|x-3|取最小值时,相应的x的值是2.
分析 (1)分别根据结论列式计算即可得解;
(2)根据结论列式距离表达式,再根据绝对值的性质计算即可得解;
(3)根据条件判断出表示x到-1、2、3这三个点的距离之和,从而判断出x在点2的位置,从而得解.
解答 解:(1)|(-3)-(-9)|=|-3+9|=6,
|2-(-8)|=|2+8|=10;
(2)由已知得,|x-(-2)|=|x+2|,
∵|AB|=4,
∴|x+2|=4,
∴x+2=4或x+2=-4,
解得x=2或x=-6;
(3)由条件可知,|x+1|+|x-2|+|x-3|表示x到-1、2、3这三个点的距离之和,
所以,当x在点2的位置时,其距离之和最小.
故答案为:(1)6,10;(2)|x+2|,2或-6;(3)2.
点评 本题考查了绝对值与数轴的知识,读懂题目信息,理解结论的并掌握数轴上两点间的距离的求法是解题的关键,也是本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2013个三角形,则这个多边形的边数为( )
| A. | 2011 | B. | 2015 | C. | 2014 | D. | 2016 |
10.方程x2=x的解是( )
| A. | x=1 | B. | x=0 | C. | x1=1 x2=0 | D. | x1=-1 x2=0 |
4.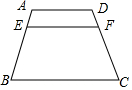 在梯形ABCD中,EF∥AD∥BC,要使梯形AEFD∽梯形EBCF,则应满足的条件是( )
在梯形ABCD中,EF∥AD∥BC,要使梯形AEFD∽梯形EBCF,则应满足的条件是( )
 在梯形ABCD中,EF∥AD∥BC,要使梯形AEFD∽梯形EBCF,则应满足的条件是( )
在梯形ABCD中,EF∥AD∥BC,要使梯形AEFD∽梯形EBCF,则应满足的条件是( )| A. | EF=$\frac{1}{2}$BC | B. | EF2=AD•BC | C. | AE=EB | D. | $\frac{AE}{AB}$=$\frac{AD}{EF}$ |




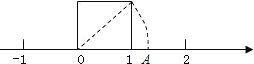 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )