题目内容
2. 两个相同的矩形ABCD和AEFG如图摆放,点E在AD上,AB=1,BC=2,连结GC,交EF于点H,连结HB,那么HB的长是$\frac{\sqrt{13}}{2}$.
两个相同的矩形ABCD和AEFG如图摆放,点E在AD上,AB=1,BC=2,连结GC,交EF于点H,连结HB,那么HB的长是$\frac{\sqrt{13}}{2}$.
分析 首先证明△FHG≌△MHC得HG=HC,利用HB=$\frac{1}{2}GC$,求出GC即可解决.
解答 解: 延长FE交BC于M,
延长FE交BC于M,
∵四边形FGBM、ABCD是矩形,
∴∠F=∠FGA=∠GBM=90°,
∴四边形FGBM是矩形,
∴FG=MB=1,∠CMH=90°
∵BC=2,∴CM=BC-BM=1,
在△FHG和△MHC中,
$\left\{\begin{array}{l}{∠FHG=∠CHM}\\{∠F=∠CMH}\\{FG=CM}\end{array}\right.$,
∴△FHG≌△MHC,
∴HG=HC,∵∠GBC=90°,
∴BH=$\frac{1}{2}$GC,
在RT△GBC中,∴GB=3,BC=2,
∴GC=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴HB=$\frac{\sqrt{13}}{2}$.
故答案为$\frac{\sqrt{13}}{2}$.
点评 本题考查矩形的性质、全等三角形的判定和性质、直角三角形斜边的中线定理,利用三角形全等是解决问题的关键.

练习册系列答案
相关题目
12.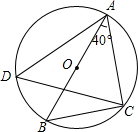 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
7.若$\frac{y}{x}=\frac{1}{4}$,则$\frac{x+2y}{x}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{2}{3}$ |
11.已知二次函数y=ax2+2x+c(a≠0)有最大值,且ac=2,则二次函数的顶点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
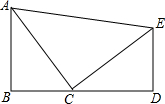 如图,AB⊥BD,ED⊥BD于D,AB=CD,AC=CE,下列结论:(1)BC=DE;(2)AC⊥CE;(3)∠CAE=45°,其中正确的有( )
如图,AB⊥BD,ED⊥BD于D,AB=CD,AC=CE,下列结论:(1)BC=DE;(2)AC⊥CE;(3)∠CAE=45°,其中正确的有( )