题目内容
5.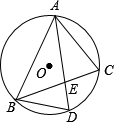 如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则AE的长为( )
如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则AE的长为( )| A. | $\frac{4}{25}$ | B. | $\frac{4}{5}$ | C. | $\frac{32}{25}$ | D. | $\frac{21}{5}$ |
分析 根据AD平分∠BAC,可得∠BAD=∠DAC,再利用同弧所对的圆周角相等,得出△ABD∽△BED,利用其对应边成比例可得$\frac{AD}{BD}$=$\frac{BD}{DE}$,然后将已知数值代入求出DE的长,进而得到AE的长.
解答 解:∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠DBC=∠DAC(同弧所对的圆周角相等),
∴∠DBC=∠BAD,
∴△ABD∽△BED,
∴$\frac{AD}{BD}$=$\frac{BD}{DE}$,
∴DE=$\frac{B{D}^{2}}{AD}$=$\frac{4}{5}$,
∴AE=AD-DE=5-$\frac{4}{5}$=$\frac{21}{5}$.
故选D.
点评 此题主要考查相似三角形的判定与性质和圆周角定理等知识点的理解和掌握,难度不大,属于基础题,要求学生应熟练掌握.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
7.若$\frac{y}{x}=\frac{1}{4}$,则$\frac{x+2y}{x}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{2}{3}$ |
14.计算3x2-2x2的结果为( )
| A. | -5x2 | B. | 5x2 | C. | -x2 | D. | x2 |
15.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)的关系如下表:
①观察上表,气温每升高5℃,音速如何变化?
②求出y与x之间的表达式;
③气温x=22℃时,某人看到烟花燃放5秒后才听到响声,那么此人与烟花燃放处的距离多远?
| 气温x(℃) | 0 | 5 | 10 | 15 | 20 |
| 音速y(米/秒) | 331 | 334 | 337 | 340 | 343 |
②求出y与x之间的表达式;
③气温x=22℃时,某人看到烟花燃放5秒后才听到响声,那么此人与烟花燃放处的距离多远?
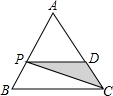 如图,P为等边三角形ABC中AB边上的动点,沿A→B的方向运动,到达点B时停止,过P作PD∥BC.设AP=x,△PDC的面积为y,则y关于x的函数图象大致为( )
如图,P为等边三角形ABC中AB边上的动点,沿A→B的方向运动,到达点B时停止,过P作PD∥BC.设AP=x,△PDC的面积为y,则y关于x的函数图象大致为( )
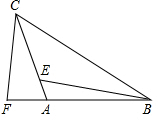 如图,在△ABC中,AB=CA,∠CAB=90°,F为BA延长线上一点,点E在线段AC上,
如图,在△ABC中,AB=CA,∠CAB=90°,F为BA延长线上一点,点E在线段AC上, 某校综合实践活动小组与5月20日(中国学生营养日)开展快餐营养情况调查活动,他们在互联网查获的食品安全监督部门的一份快餐信息如图所示,请根据此信息,解答下列问题:
某校综合实践活动小组与5月20日(中国学生营养日)开展快餐营养情况调查活动,他们在互联网查获的食品安全监督部门的一份快餐信息如图所示,请根据此信息,解答下列问题: