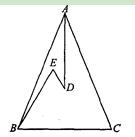
��Ŀ����
��֪����ƽ��ֱ������ϵxoy�У�������y=ax2��bx��c��ֱ��y=mx��n�ཻ��
A(0���� ),B(m��b��m2��mb��n)����,����a��b��c��m��n��Ϊʵ������a��0��m��0
),B(m��b��m2��mb��n)����,����a��b��c��m��n��Ϊʵ������a��0��m��0
(1) ����գ�c= ��n= ��
����a��ֵ��
С��˼������B(m��b��m2��mb��n) ��������y=ax2��bx��c��
��m2��mb��n=a(m��b)2+b(m��b)+c
����
�����С���Ľ������ֱ��д��a ��ֵ��a = ___________.
(2) ��m=1��b=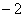 ,���P��������y=ax2��bx��c�ϣ�����ֱ��AB���·������ABP
,���P��������y=ax2��bx��c�ϣ�����ֱ��AB���·������ABP
�����ȡֵ��Χ��
(3) ��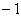 �� x ��1ʱ����������y=ax2��bx��c�ϵ�x��������ĵ�����ꡣ���ú�b�Ĵ���ʽ��ʾ��
�� x ��1ʱ����������y=ax2��bx��c�ϵ�x��������ĵ�����ꡣ���ú�b�Ĵ���ʽ��ʾ��
 |
.(1) n=�� ,c=��
,c=�� (2��)
(2��)
a =1(4��)
(2) ��m=1��b=��2,��ֱ��:y=x- ;�����ߣ�y=x2��2x-
;�����ߣ�y=x2��2x-
��ABP��������ֵΪ (8��)
(8��)
(3) ������y=x2+bx- �ĶԳ���Ϊx=��
�ĶԳ���Ϊx=�� ,��СֵΪ��
,��СֵΪ��
 ��x=��1ʱ��y=
��x=��1ʱ��y= ��b����x=1ʱ��y=
��b����x=1ʱ��y= +b(9��)
+b(9��)
�� ��x=�� �ܣ�1����b��2ʱ��
�ܣ�1����b��2ʱ��
︱ +b︱-︱
+b︱-︱ -b︱=
-b︱= +b+
+b+ -b=1��0
-b=1��0
��x��������ĵ������Ϊ(1�� +b)(10��)
+b)(10��)
�ڵ���1���� ��0����0��b��2ʱ
��0����0��b��2ʱ
︱ +b︱-︱-
+b︱-︱- ︱=
︱= +b-
+b- =b(1-
=b(1- )��0
)��0
�ൽx��������ĵ������Ϊ(1�� +b)(11��)
+b)(11��)
�۵�0���� ��1����-2��b��0ʱ
��1����-2��b��0ʱ
︱ -b︱-︱-
-b︱-︱- ︱=
︱= -b-
-b- =-b(1+
=-b(1+ )��0
)��0
�ൽx��������ĵ������Ϊ(-1�� -b)(12��)
-b)(12��)
�ܵ�x=�� ��1����b��-2ʱ��
��1����b��-2ʱ��
︱ +b︱-︱
+b︱-︱ -b︱=-
-b︱=- -b-(
-b-( -b)=-1��0
-b)=-1��0
�ൽx��������ĵ������Ϊ(-1�� -b)(13��)
-b)(13��)
������������b��0ʱ����x��������ĵ������Ϊ(1�� +b)��
+b)��
��b��0ʱ����x��������ĵ������Ϊ(-1�� -b).
-b).

�ס���������е��Ժ��������ٶȱ���������ѧ��ÿ�������뺺�ֵĸ�����ͳ�Ƽ���������±���
| �� �� | �μ����� | ��λ�� | ���� | ƽ������ |
| �� | 55 | 149 | 191 | 135 |
| �� | 55 | 151 | 110 | 135 |
ijͬѧ�����ϱ������ó����½��ۣ�(1)�ס�������ѧ���ɼ���ƽ��ˮƽ��ͬ��(2)�Ұ�������������ڼװ����������(ÿ�������뺺������150��Ϊ����)��(3)�װ�ɼ����Ұ�ɼ�����������������ȷ����( )
A��(1)(2)(3) B��(1)(2) C��(1)(3) D��(2)(3)
���κ���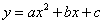 ��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
| X | ﹣1 | 0 | 1 | 3 |
| y | ﹣1 | 3 | 5 | 3 |
���н��ۣ�
��1��ac��0����2����x��1ʱ��y��ֵ��xֵ���������С��
��3��3�Ƿ���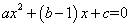 ��һ������
��һ������
��4����﹣1��x��3ʱ��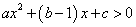 ��
��
������ȷ�ĸ���Ϊ��������
�� A��4�� B��3�� C��2�� D��1��
 B.
B.  C.
C.  D.
D. 
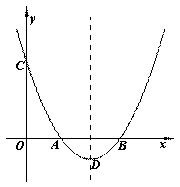
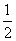 (x��3)2��1��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C������ΪD.
(x��3)2��1��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C������ΪD. 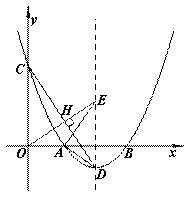
 �ϣ�AB=10cm����B�İ뾶Ϊ1cm,��C��ֱ��
�ϣ�AB=10cm����B�İ뾶Ϊ1cm,��C��ֱ��