题目内容
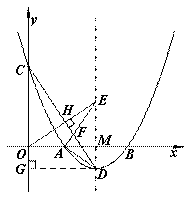
如图,抛物线y=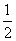 (x-3)2-1与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(x-3)2-1与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)试求点A、B、D的坐标;
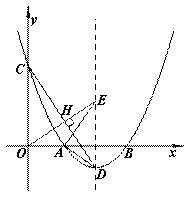
(2)连接CD,过原点O作OE⊥CD于点H,OE与抛物线的对称轴交于点E,连接AE、AD.求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙O的切线,切点为Q,当PQ的长最小时,求点P的坐标.
解:(1)由y=0得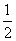 (x-3)2-1=0,解得x1=3-
(x-3)2-1=0,解得x1=3-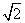 ,x2=3+
,x2=3+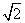 ,又点A在点B的左侧,∴A点坐标为(3-
,又点A在点B的左侧,∴A点坐标为(3-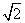 ,0),B点坐标为(3+
,0),B点坐标为(3+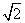 ,0),由抛物线解析式y=
,0),由抛物线解析式y=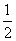 (x-3)2-1可得顶点D的坐标为(3,﹣1).
(x-3)2-1可得顶点D的坐标为(3,﹣1).
(2)如下图,过点D作DG⊥y轴于点G,∵∠DCG=∠EOM,∠CGD=∠OME=90°,∴△CDG∽△OEM,∴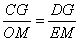 ,即
,即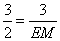 ,∴解得EM=2,∴E点坐标为(3,2),ED=2+1=3,在Rt△AEM中,由勾股定理得AE2=EM2+AM2=22+[3-(3-
,∴解得EM=2,∴E点坐标为(3,2),ED=2+1=3,在Rt△AEM中,由勾股定理得AE2=EM2+AM2=22+[3-(3-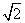 )]2=6,在Rt△ADM中,由勾股定理得AD2=DM2+AM2=12+[3-(3-
)]2=6,在Rt△ADM中,由勾股定理得AD2=DM2+AM2=12+[3-(3-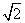 )]2=3,∴AE2+AD2=6+3=9=32=ED2,∴△AED是直角三角形,即∠DAE=90°.设AE交CD于点F,∴∠ADC+∠AFD=90°,又∵∠AEO+∠HFE=90°,∠AFD=∠HFE,∴∠AEO=∠ADC.
)]2=3,∴AE2+AD2=6+3=9=32=ED2,∴△AED是直角三角形,即∠DAE=90°.设AE交CD于点F,∴∠ADC+∠AFD=90°,又∵∠AEO+∠HFE=90°,∠AFD=∠HFE,∴∠AEO=∠ADC.
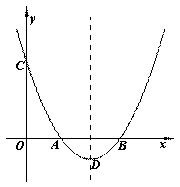
(3)如下图,由⊙E的半径为1,由勾股定理得PQ2=EP2-1,要使切线长PQ最小,只需EP长最小,即EP2最小.设P点坐标为(x,y),则PQ=x-3,EQ=2-y,∴由勾股定理得EP2=(x-3)2+(2-y)2,∵y=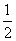 (x-3)2-1,∴(x-3)2=2y+2,∴EP2=2y+2+y2-4y+4=(y-1)2+5,当y=1时,EP2最小值为5.把y=1代入y=
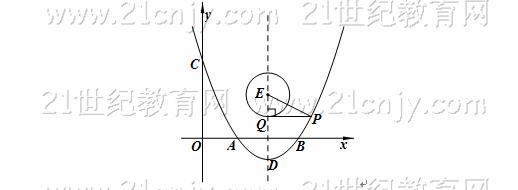
(x-3)2-1,∴(x-3)2=2y+2,∴EP2=2y+2+y2-4y+4=(y-1)2+5,当y=1时,EP2最小值为5.把y=1代入y=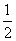 (x-3)2-1得
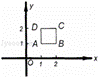
(x-3)2-1得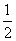 (x-3)2-1=1,解得x1=1,x2=5,又∵点P在对称轴右侧的抛物线上,∴x1=1不合题意,舍去,∴点P的坐标为(5,1).
(x-3)2-1=1,解得x1=1,x2=5,又∵点P在对称轴右侧的抛物线上,∴x1=1不合题意,舍去,∴点P的坐标为(5,1).

 53随堂测系列答案
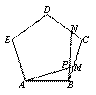
53随堂测系列答案 的纸条如图放置.已知∠1=30°,则∠2的度数为( )
的纸条如图放置.已知∠1=30°,则∠2的度数为( )
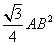 .其中正确的结论有…………………………………【 】
.其中正确的结论有…………………………………【 】 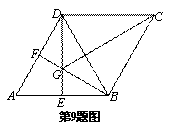
 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是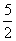 B.x≥
B.x≥ C.x≥
C.x≥ ),B(m-b,m2-mb+n)两点,其中a,b,c,m,n均为实数,且a≠0,m≠0
),B(m-b,m2-mb+n)两点,其中a,b,c,m,n均为实数,且a≠0,m≠0 ,设点P在抛物线y=ax2+bx+c上,且在直线AB的下方,求△ABP
,设点P在抛物线y=ax2+bx+c上,且在直线AB的下方,求△ABP ≤ x ≤1时,求抛物线y=ax2+bx+c上到x轴距离最大的点的坐标。(用含b的代数式表示)
≤ x ≤1时,求抛物线y=ax2+bx+c上到x轴距离最大的点的坐标。(用含b的代数式表示)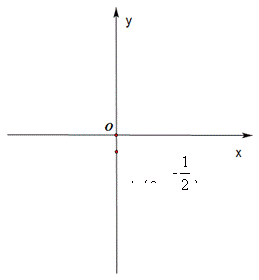
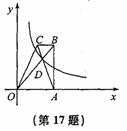
 经过点D,若AO=2BC,△BCD的面积为3,则k的值为_______.
经过点D,若AO=2BC,△BCD的面积为3,则k的值为_______.