题目内容
在直角坐标系中,A (-6,0),B在第二象限,AOB为等边三角形.BE⊥y轴与y轴相交于点E,F在第一象限,△EOF为等边三角形.连接AF.求证:PA=PF.(不能用四点共圆、三角函数、相似三角形解题)
考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:易证点B坐标,即可求得点E坐标,根据等边三角形的性质即可求得点F的坐标,即可求得直线AF的解析式,即可求得点P的坐标,即可解题.
解答:解:找到AO中点M,OE中点N,连接BM,FN,

∵△AOB为等边三角形,AM=3,
∴BM=3
,
∴点B横坐标为-3,纵坐标为3
,
∴点E坐标为(0,3
),
∵△EOF为等边三角形,ON=
,
∴FN=
,
∴F点坐标为(
,
)
设直线AF解析式为y=kx+b,代入A,F得:y=
x+
,
设直线OB解析式为y=kx+b,代入O,B得:y=-
x,
∴交点P坐标为(-
,
).
∴AP=PF.

∵△AOB为等边三角形,AM=3,
∴BM=3
| 3 |
∴点B横坐标为-3,纵坐标为3
| 3 |
∴点E坐标为(0,3
| 3 |
∵△EOF为等边三角形,ON=
3
| ||
| 2 |
∴FN=
| 9 |
| 2 |
∴F点坐标为(
| 9 |
| 2 |
3
| ||
| 2 |
设直线AF解析式为y=kx+b,代入A,F得:y=
| ||
| 7 |
6
| ||
| 7 |
设直线OB解析式为y=kx+b,代入O,B得:y=-
| 3 |
∴交点P坐标为(-
| 3 |
| 4 |
3
| ||
| 4 |
∴AP=PF.
点评:本题考查了等边三角形三线合一的性质,考查了一次函数在平面直角坐标系中运用,本题中求得直线AF的解析式是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
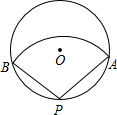 如图,在一个半径为2
如图,在一个半径为2 如图是一个圆锥和一个圆柱的组合体盖子,已知它的半径为30cm,圆柱体高2cm,锥高8cm,求它的全面积.(结果保留一位小数)
如图是一个圆锥和一个圆柱的组合体盖子,已知它的半径为30cm,圆柱体高2cm,锥高8cm,求它的全面积.(结果保留一位小数)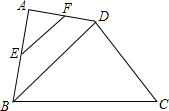 在四边形ABCD中,BD是对角线,E,F分别是AB,AD的中点,若EF=2,tan∠DBC=
在四边形ABCD中,BD是对角线,E,F分别是AB,AD的中点,若EF=2,tan∠DBC=