题目内容
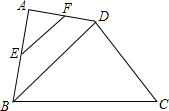在四边形ABCD中，BD是对角线，E，F分别是AB，AD的中点，若EF=2，tan∠DBC=| 3 |
| 4 |
考点：勾股定理
专题：计算题
分析：作DG⊥BC，交BC于点G，由EF为三角形ABD中位线，求出BD的长，在三角形BDG中，利用锐角三角函数定义及tan∠DBC的值，设出DG与BG，利用勾股定理求出x的值，确定出DG与BG的长，在直角三角形DGC中，利用勾股定理求出GC的长，由BG+GC求出BC的长即可．
解答：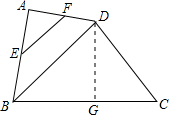
解：作DG⊥BC，交BC于点G，
∵E、F分别为AB、AD的中点，
∴EF为△ABD的中位线，即BD=2EF=4，
在Rt△BDG中，tan∠DBC=
=
，设DG=3x，BG=4x，
根据勾股定理得：BD=
=5x=4，
解得：x=
，
∴DG=2.4，BG=3.2，
在Rt△DGC中，DC=3，DG=
，
根据勾股定理得：GC=
=1.8，
则BC=BG+GC=3.2+1.8=5．
解：作DG⊥BC，交BC于点G，∵E、F分别为AB、AD的中点，
∴EF为△ABD的中位线，即BD=2EF=4，
在Rt△BDG中，tan∠DBC=
| DG |
| BG |
| 3 |
| 4 |
根据勾股定理得：BD=
| DG2+BG2 |
解得：x=
| 4 |
| 5 |
∴DG=2.4，BG=3.2，
在Rt△DGC中，DC=3，DG=
| 12 |
| 5 |
根据勾股定理得：GC=
| CD2-DG2 |
则BC=BG+GC=3.2+1.8=5．
点评：此题考查了勾股定理，以及锐角三角函数定义，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
如果线段a，b，c，d满足ad=bc，则下列各式中不成立的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
四边形ABCD是圆内接四边形，AC是直径，BD是∠ABC的角平分线，AB+BC=6，求四边形ABCD的面积．