题目内容
在菱形ABCD中,对角线AC、BD相交于点O,其中AC=8,BD=6,则sin∠BAD的值为 .
考点:菱形的性质
专题:
分析:由菱形ABCD中对角线AC、BD相交于点O,若AC=8,BD=6,即可求得OA与OB的长,然后由股定理求得菱形的边长,根据面积公式求出BE,即可得出答案.
解答:解:过B作BE⊥AD于E,
∵四边形ABCD是菱形,且AC=8,BD=6,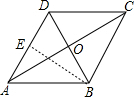
∴OA=
AB=4,OB=
BD=3,AC⊥BD,
∴AB=
=5,
即AD=AB=5,
∵由面积公式得:AD×BE=
×BD×AC,
∴5AE=
×6×8,
∴BE=
,
∴在Rt△ABE中,sin∠BAD=
=
=
,
故答案为:
.
∵四边形ABCD是菱形,且AC=8,BD=6,

∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| OA2+OB2 |
即AD=AB=5,
∵由面积公式得:AD×BE=
| 1 |
| 2 |
∴5AE=
| 1 |
| 2 |
∴BE=
| 24 |
| 5 |
∴在Rt△ABE中,sin∠BAD=
| BE |
| AB |
| ||
| 5 |
| 24 |
| 25 |
故答案为:
| 24 |
| 25 |
点评:此题考查了菱形的性质以及勾股定理,解直角三角形,关键是正确作辅助线并求出BE的长,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
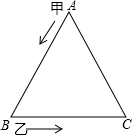 如图,甲乙两人同时沿着边长为30米的等边三角形,按逆时针的方向行走,甲从A以65米/分的速度,乙从B以71米/分的速度行走,当乙第一次追上甲时在等边三角形的( )
如图,甲乙两人同时沿着边长为30米的等边三角形,按逆时针的方向行走,甲从A以65米/分的速度,乙从B以71米/分的速度行走,当乙第一次追上甲时在等边三角形的( )| A、AB边上 | B、点B处 |
| C、BC边上 | D、AC边上 |
和一个已知点P的距离等于3cm的直线可以画( )
| A、1条 | B、2条 | C、3条 | D、无数条 |
若A和B都是五次多项式,则( )
| A、A+B一定是多项式 |
| B、A-B一定是单项式 |
| C、A-B是次数不高于5的整式 |
| D、A+B是次数不低于5的整式 |
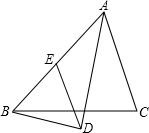 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC交AB于E.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC交AB于E.