题目内容
7.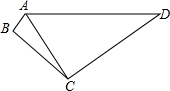 如图所示,AB⊥BC,AB=7,BC=24,CD=60,AD=65,求△ACD的面积.
如图所示,AB⊥BC,AB=7,BC=24,CD=60,AD=65,求△ACD的面积.
分析 先由勾股定理求出AC,再由勾股定理的逆定理证明△ACD是直角三角形,∠ACD=90°,△ACD的面积=$\frac{1}{2}$×AC×CD,即可得出结果.
解答 解:∵AB⊥BC,
∴∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{7}^{2}+2{4}^{2}}$=25,
∵252+602=652,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°,
∴△ACD的面积=$\frac{1}{2}$×AC×CD=$\frac{1}{2}$×25×60=750.
点评 本题考查了勾股定理、勾股定理的逆定理;熟练掌握勾股定理和勾股定理的逆定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.近似数0.60的准确值a的取值范围是( )
| A. | 0.555≤a<0.655 | B. | 0.55≤a≤0.65 | C. | 0.595<a≤0.605 | D. | 0.595≤a<0.605 |
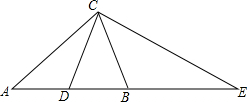 如图所示,已知在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE,请判断CD与CE的长度有何关系,并证明你的结论.
如图所示,已知在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE,请判断CD与CE的长度有何关系,并证明你的结论.