题目内容
15．
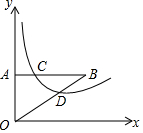如图，△AOB与反比例函数y=$\frac{k}{x}$交于C、D，△AOB的面积为6，若AC：BC=1：3，则反比例函数的表达式为y=$\frac{3}{x}$．
分析 连接OC，根据△AOB的面积为6，AC：BC=1：3可得出△AOC的面积，进而可得出结论．
解答 
解：连接OC，
∵△AOB的面积为6，AC：BC=1：3，
∴S△AOC=$\frac{1}{4}$×6=1.5，
∴k=2×1.5=3，
∴反比例函数的表达式为：y=$\frac{3}{x}$．
故答案为：y=$\frac{3}{x}$．
点评 本题考查的是反比例函数系数k的几何意义，熟知在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|，且保持不变是解答此题的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
6．在△ABC中，AB=15，AC=13，高AD=12，则△ABC中BC边的长为（ ）
| A． | 9 | B． | 5 | C． | 14 | D． | 4或14 |
如图，a∥b，∠2=∠3，∠1=40°，则∠4的度数是40度．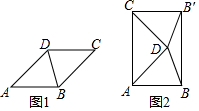
如图1，将1张菱形纸片ABC的（∠ADC＞90°）沿对角线BD剪开，得到△ABD和△BCD．再将△BCD以D为旋转中心，按逆时针方向旋转角α，使α=∠ADB，得到如图2所示的△DB′C，连接AC、BB′，∠DAB=45°，有以下结论：①AC=BB′；②AC⊥AB；③∠CDA=90°；④BB′=$\sqrt{3}$AB，其中正确结论的序号是①②③．（把所有正确结论的序号都填在横线上）
7．
由五个相同的正方体搭成的几何体如图所示，则它的俯视图是（ ）
由五个相同的正方体搭成的几何体如图所示，则它的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
4．
如图，在?ABCD中，AB=2，BC=4，∠D=60°，点P、Q分别是AC和BC上的动点，在点P和点Q运动的过程中，PB+PQ的最小值为（ ）
如图，在?ABCD中，AB=2，BC=4，∠D=60°，点P、Q分别是AC和BC上的动点，在点P和点Q运动的过程中，PB+PQ的最小值为（ ）| A． | 4 | B． | 3 | C． | 2$\sqrt{3}$ | D． | 4$\sqrt{3}$ |
（1）化简：（x+1）2-x（2-x）