题目内容
20.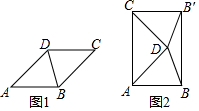 如图1,将1张菱形纸片ABC的(∠ADC>90°)沿对角线BD剪开,得到△ABD和△BCD.再将△BCD以D为旋转中心,按逆时针方向旋转角α,使α=∠ADB,得到如图2所示的△DB′C,连接AC、BB′,∠DAB=45°,有以下结论:①AC=BB′;②AC⊥AB;③∠CDA=90°;④BB′=$\sqrt{3}$AB,其中正确结论的序号是①②③.(把所有正确结论的序号都填在横线上)
如图1,将1张菱形纸片ABC的(∠ADC>90°)沿对角线BD剪开,得到△ABD和△BCD.再将△BCD以D为旋转中心,按逆时针方向旋转角α,使α=∠ADB,得到如图2所示的△DB′C,连接AC、BB′,∠DAB=45°,有以下结论:①AC=BB′;②AC⊥AB;③∠CDA=90°;④BB′=$\sqrt{3}$AB,其中正确结论的序号是①②③.(把所有正确结论的序号都填在横线上)
分析 如图1,先利用菱形的性质得AB=BC=CD=AD,∠A=∠C=45°,则利用等腰三角形的性质和三角形内角和可计算出∠ADB=∠ABD=67.5°,则α=2∠ADB=135°;如图2,利用旋转的性质得到DB=DB′,DC=DA,CB′=AB,∠7=∠3=67.5°,∠6=135°,则可计算出∠4=∠5=22.5°,所以∠ABB′=∠BB′C=90°,则可证明四边形ABB′C为矩形,于是可对①②进行判断;然后证明△ADC为等腰直角三角形,则可对③④进行判断.
解答 解:如图1,
∵四边形ABCD为菱形,
∴AB=BC=CD=AD,∠A=∠C=45°,
∴∠ADB=∠ABD=67.5°,
∴α=2∠ADB=135°,
如图2,
∵将△BCD以D为旋转中心,按逆时针方向旋转角135°,
∴DB=DB′,DC=DA,CB′=AB,∠7=∠3=67.5°,∠6=135°,
在△DBB′中,∠4=∠5=$\frac{1}{2}$(180°-135°)=22.5°,
∴∠ABB′=∠3+∠4=90°,∠BB′C=∠5+∠7=90°,
∴AB∥CB′,
而AB=CB′,
∴四边形ABB′C为矩形,
∴AC=BB′,AC⊥AB,所以①②正确,
∵∠CAB=90°,∠1=45°,
∴∠CAD=45°,
而DC=DA,
∴△ADC为等腰直角三角形,
∴∠CDA=90°;BB′=$\sqrt{2}$AB,所以③正确,④错误.
故答案为①②③.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了矩形的判定与性质和菱形的性质.

练习册系列答案
相关题目
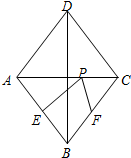 如图,在菱形ABCD中,对角线AC=6,BD=8,点E是边AB的中点,点F、P分别是BC、AC上动点,则PE+PF的最小值是$\frac{24}{5}$.
如图,在菱形ABCD中,对角线AC=6,BD=8,点E是边AB的中点,点F、P分别是BC、AC上动点,则PE+PF的最小值是$\frac{24}{5}$.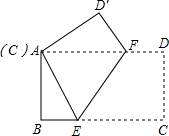 如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则EF长为$\frac{15}{2}$cm.
如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则EF长为$\frac{15}{2}$cm.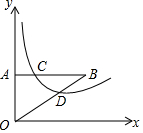 如图,△AOB与反比例函数y=$\frac{k}{x}$交于C、D,△AOB的面积为6,若AC:BC=1:3,则反比例函数的表达式为y=$\frac{3}{x}$.
如图,△AOB与反比例函数y=$\frac{k}{x}$交于C、D,△AOB的面积为6,若AC:BC=1:3,则反比例函数的表达式为y=$\frac{3}{x}$.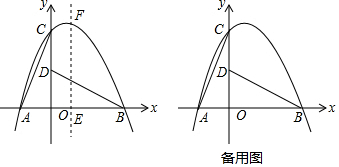
 小明对九(1)班全班同学“你最喜欢的球类项目是什么?(只选一项)”的问题进行了调查,把所得数据绘制成如图所示的扇形统计图,由图可知,“乒乓球”对应的扇形的圆心角度数是72度.
小明对九(1)班全班同学“你最喜欢的球类项目是什么?(只选一项)”的问题进行了调查,把所得数据绘制成如图所示的扇形统计图,由图可知,“乒乓球”对应的扇形的圆心角度数是72度.