题目内容
6.在△ABC中,AB=15,AC=13,高AD=12,则△ABC中BC边的长为( )| A. | 9 | B. | 5 | C. | 14 | D. | 4或14 |
分析 分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=BD-CD.
解答 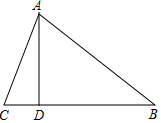 解:(1)如图,锐角△ABC中,AC=13,AB=15,BC边上高AD=12,
解:(1)如图,锐角△ABC中,AC=13,AB=15,BC边上高AD=12,
∵在Rt△ACD中AC=13,AD=12,
∴CD2=AC2-AD2=132-122=25,
∴CD=5,
在Rt△ABD中AB=15,AD=12,由勾股定理得
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为BD+DC=9+5=14;
(2)钝角△ABC中,AC=13,AB=15,BC边上高AD=12,
在Rt△ACD中AC=13,AD=12,由勾股定理得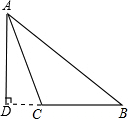
CD2=AC2-AD2=132-122=25,
∴CD=5,
在Rt△ABD中AB=15,AD=12,由勾股定理得
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为DB-BC=9-5=4.
故选:D.
点评 本题考查了勾股定理,把三角形斜边转化到直角三角形中用勾股定理解答.关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
17.下列说法中,正确的是( )
| A. | 无理数包括正无理数、零和负无理数 | |
| B. | 无限小数都是无理数 | |
| C. | 正实数包括正有理数和正无理数 | |
| D. | 实数可以分为正实数和负实数两类 |
18.点C在x轴上方,y轴左侧,距离x轴2个单位长度,距离y轴3个单位长度,则点C的坐标为( )
| A. | (-3,2) | B. | (-2,-3) | C. | (-2,3) | D. | ( 3,-2) |
 如图,?ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AB的长是1,则EF=$\sqrt{3}$.
如图,?ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AB的长是1,则EF=$\sqrt{3}$. 如图,A,B两点的坐标分别为(-3,5),(3,5),点C在同一坐标系下的坐标为(-1,7).
如图,A,B两点的坐标分别为(-3,5),(3,5),点C在同一坐标系下的坐标为(-1,7).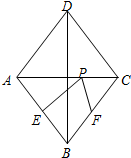 如图,在菱形ABCD中,对角线AC=6,BD=8,点E是边AB的中点,点F、P分别是BC、AC上动点,则PE+PF的最小值是$\frac{24}{5}$.
如图,在菱形ABCD中,对角线AC=6,BD=8,点E是边AB的中点,点F、P分别是BC、AC上动点,则PE+PF的最小值是$\frac{24}{5}$.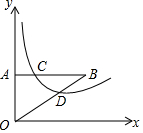 如图,△AOB与反比例函数y=$\frac{k}{x}$交于C、D,△AOB的面积为6,若AC:BC=1:3,则反比例函数的表达式为y=$\frac{3}{x}$.
如图,△AOB与反比例函数y=$\frac{k}{x}$交于C、D,△AOB的面积为6,若AC:BC=1:3,则反比例函数的表达式为y=$\frac{3}{x}$.