题目内容
2. 如图,已知矩形ABCD中,AB=6cm,BC=8cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长等于20cm.
如图,已知矩形ABCD中,AB=6cm,BC=8cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长等于20cm.
分析 连接AC、BD,根据三角形的中位线求出HG、GF、EF、EH的长,再求出四边形EFGH的周长即可.
解答 解:如图,连接AC、BD,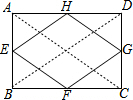
∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AC=BD=$\sqrt{{6}^{2}+{8}^{2}}$=10(cm),
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HG=EF=$\frac{1}{2}$AC=5cm,EH=FG=$\frac{1}{2}$BD=5cm,
∴四边形EFGH的周长等于:5×4=20(cm_,
故答案为:20.
点评 本题考查了矩形的性质,三角形的中位线的应用,能求出四边形的各个边的长是解此题的关键,注意:矩形的对角线相等,三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.△ABC是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB=50米,如果要在这块空地上种植草皮,按每平方米草皮a元计算,那么共需要资金( )
| A. | 600a元 | B. | 50a元 | C. | 1200a元 | D. | 1500a元 |
13. 如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,M,N分别是线段BC,AB上的动点,(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,M,N分别是线段BC,AB上的动点,(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则EF长度的最大值为( )
 如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,M,N分别是线段BC,AB上的动点,(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,M,N分别是线段BC,AB上的动点,(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则EF长度的最大值为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
17.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用
(Ⅰ)若每年去该健身中心6次,应选择哪种消费方式更合算?
(Ⅱ)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(Ⅲ)若某位顾客每年去该健身中心健身至少18次,请通过计算帮助这位顾客选择最合算的消费方式.
| 消费卡 | 消费方式 |
| 普通卡 | 35元/次 |
| 白金卡 | 280元/张,凭卡免费消费10次再送2次 |
| 钻石卡 | 560元/张,凭卡每次消费不再收费 |
(Ⅰ)若每年去该健身中心6次,应选择哪种消费方式更合算?
(Ⅱ)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(Ⅲ)若某位顾客每年去该健身中心健身至少18次,请通过计算帮助这位顾客选择最合算的消费方式.
7.已知直线MN垂直于x轴,若点M的坐标为(-5,2),点N距x轴的距离为3个单位,则点N的坐标为( )
| A. | (-5,3) | B. | (-5,3)或(-5,-3) | C. | (3,2) | D. | (3,2)或(-3,2) |
11.下列运算正确的是( )
| A. | 3a-a=2 | B. | a•a2=a3 | C. | a6÷a3=a2 | D. | (a3)2=a5 |
 如图,在边长为8的正方形ABCD中,E是AB上的点,⊙O是以BC为直径的圆.
如图,在边长为8的正方形ABCD中,E是AB上的点,⊙O是以BC为直径的圆.