题目内容
13. 如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,M,N分别是线段BC,AB上的动点,(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,M,N分别是线段BC,AB上的动点,(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则EF长度的最大值为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
分析 根据三角形的中位线定理得出EF=$\frac{1}{2}$DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,此时根据勾股定理求得DN=DB=6,从而求得EF的最大值为3.
解答 解:∵ED=EM,MF=FN,
∴EF=$\frac{1}{2}$DN,
∴DN最大时,EF最大,
∵N与B重合时DN最大,
此时DN=DB=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{3}^{2}+(3\sqrt{3})^{2}}$=6,
∴EF的最大值为3.
故选B.
点评 本题考查了三角形中位线定理,勾股定理的应用,熟练掌握定理是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
4.方程组$\left\{\begin{array}{l}{x+y=5}\\{x-y=1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ |
1. 小明同学把一个含有45°角的三角板放在如图所示两条平行线m、n上,测得∠β=70°,则∠α的度数是( )
小明同学把一个含有45°角的三角板放在如图所示两条平行线m、n上,测得∠β=70°,则∠α的度数是( )
 小明同学把一个含有45°角的三角板放在如图所示两条平行线m、n上,测得∠β=70°,则∠α的度数是( )
小明同学把一个含有45°角的三角板放在如图所示两条平行线m、n上,测得∠β=70°,则∠α的度数是( )| A. | 105° | B. | 110° | C. | 115° | D. | 125° |
18. 如图,在下面的条件中,不能判定l1∥l2的是( )
如图,在下面的条件中,不能判定l1∥l2的是( )
 如图,在下面的条件中,不能判定l1∥l2的是( )
如图,在下面的条件中,不能判定l1∥l2的是( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | ∠2+∠4=180° | D. | ∠4+∠5=180° |
5.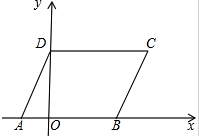 如图所示,平行四边形ABCD中,顶点A,B,D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为( )
如图所示,平行四边形ABCD中,顶点A,B,D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为( )
 如图所示,平行四边形ABCD中,顶点A,B,D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为( )
如图所示,平行四边形ABCD中,顶点A,B,D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为( )| A. | (6,5) | B. | (9,4) | C. | (6,4) | D. | (9,5) |
3.下列式子正确的是( )
| A. | $\root{3}{-6}=-\root{3}{6}$ | B. | $±\sqrt{16}=4$ | C. | $\sqrt{25}$=±5 | D. | $\sqrt{(-3)^{2}}$=-3 |
 已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且∠AQP=90°.
已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且∠AQP=90°. 如图,已知矩形ABCD中,AB=6cm,BC=8cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长等于20cm.
如图,已知矩形ABCD中,AB=6cm,BC=8cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长等于20cm.