Question

8．课间，顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内（如图），已知直角顶点H的坐标为（0，1），另一个顶点G的坐标为（4，4），则点K的坐标为（3，-3）．

Answer 1

分析 根据余角的性质，可得∠GHP=∠HKQ，根据全等三角形的判定与性质，可得KQ，HQ，根据线段的和差，可得OQ，可得答案．

解答 解：作GP⊥y轴，KQ⊥y轴，如图，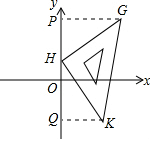
∴∠GPH=∠KQH=90°
∵GH=KH，∠GHK=90°，
∴∠GHP+∠KHQ=90°．
又∠HKQ+∠KHQ=90°
∴∠GHP=∠HKQ．
在△GPH和△HQK中，
$\left\{\begin{array}{l}{∠GPH=∠HQK}\\{∠GHP=∠HKQ}\\{GH=KH}\end{array}\right.$
Rt△GPH≌Rt△KHQ（AAS），
KQ=PH=4-1=3；HQ=GP=4．
∵QO=QH-HO=4-1=3，
∴K（3，-3），
故答案为：（3，-3）．

点评 本题考查了全等三角形的判定与性质，利用全等三角形的判定与性质得出KQ，HQ是解题关键．