题目内容
两圆的圆心距为6,它们的半径分别是一元二次方程x2-5x+6=0的两根,则两圆( )
| A、外切 | B、相交 | C、内切 | D、外离 |
考点:圆与圆的位置关系,解一元二次方程-因式分解法
专题:
分析:解答此题,先由一元二次方程的两根关系,得出两圆半径之和,然后根据圆与圆的位置关系判断条件,确定位置关系.设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R-r<d<R+r;内切,则d=R-r;内含,则d<R-r.
解答:解:设两圆半径分别为R、r,依题意得R+r=5,
又∵圆心距d=6,
∴两圆相交.
故选B.
又∵圆心距d=6,
∴两圆相交.
故选B.
点评:此题综合考查一元二次方程根与系数之间的关系及两圆的位置关系的判断.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
甲对乙说:“当我的岁数是你现在的岁数时,你才4岁.”乙对甲说:“当我的岁数是你现在的岁数时,你将61岁了.”则甲现在的岁数是( )
| A、24岁 | B、36岁 |
| C、42岁 | D、无法确定 |
下列图案是轴对称图形的有( )个.


| A、1 | B、2 | C、3 | D、4 |
下列各式中计算正确的是( )
A、(
| ||
| B、a2•a3=a6 | ||
| C、(-3a-3)2=9a6 | ||
| D、a5+a3=a8 |
某次射击练习中,甲、乙两名同学的成绩(单位:环)如表,则这两名同学射击成绩的方差( )
| 选手 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
| 甲 | 5 | 6 | 8 | 7 | 9 |
| 乙 | 6 | 7 | 4 | 10 | 8 |
| A、甲的方差大 |
| B、乙的方差大 |
| C、甲、乙的方差一样大 |
| D、甲、乙的方差无法判断大小 |
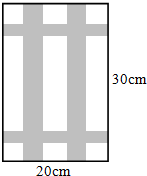 如图,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形面积的三分之一,设每个横彩条的宽为2x,则下列方程正确的是( )
如图,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形面积的三分之一,设每个横彩条的宽为2x,则下列方程正确的是( )A、(20-3x)(30-2x)=(1-
| ||
B、(20-6x)(30-4x)=
| ||
C、(20-6x)(30-4x)=(1-
| ||
D、(20-2x)(20-3x)=(1-
|