题目内容
8.若直线y=kx和双曲线y=$\frac{4}{x}$交于A(x1,y1),B(x2,y2)两点,那么(x1-2x2)(2y1-y2)=36.分析 由y=$\frac{4}{x}$知x1y1=x2y2=4,由kx=$\frac{4}{x}$得到x1=$\frac{2\sqrt{k}}{k}$、y1=2$\sqrt{k}$、x2=-$\frac{2\sqrt{k}}{k}$、y2=-2$\sqrt{k}$,代入原式=2x1y1-x1y2-4x2y1+2x2y2可得答案.
解答 解:根据题意得:kx=$\frac{4}{x}$,
则kx2=4,即x2=$\frac{4}{{k}^{2}}$,
则x1=$\frac{2\sqrt{k}}{k}$,此时y1=$\frac{4}{\frac{2\sqrt{k}}{k}}$=2$\sqrt{k}$,
x2=-$\frac{2\sqrt{k}}{k}$,y2=-2$\sqrt{k}$,
∴原式=2x1y1-x1y2-4x2y1+2x2y2
=2×4+$\frac{2\sqrt{k}}{k}$•2$\sqrt{k}$+4•$\frac{2\sqrt{k}}{k}$•2$\sqrt{k}$+2×4
=8+4+16+8
=36,
故答案为:36.
点评 本题考查了一次函数与反比例函数的解析式,正确求得x1、x2以及对应的y1和y2的值是关键.

练习册系列答案
相关题目
7.若关于x的不等式组$\left\{\begin{array}{l}{2x-3<4x+5}\\{x-a>1}\end{array}\right.$的解集是x>-4,则a的取值范围是( )
| A. | a>-4 | B. | a<-5 | C. | a≥-5 | D. | a≤-5 |
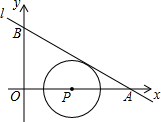 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3$\sqrt{3}$与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是4.
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3$\sqrt{3}$与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是4.