题目内容
12.(1)计算:($\frac{1}{2}$)-2+$\sqrt{4}$-2cos60°;(2)先化简,再求值:(a-$\frac{1}{a}$)÷$\frac{a+1}{a}$,其中a=$\sqrt{3}$+1.
分析 (1)分别根据负整数指数幂的计算法则、特殊角的三角函数值及数的开方法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x=2代入进行计算即可.
解答 解:(1)原式=4+2-2×$\frac{1}{2}$
=6-1
=5;
(2)原式=$\frac{(a+1)(a-1)}{a}$•$\frac{a}{a+1}$
=a-1,
当a=$\sqrt{3}$+1时,原式=$\sqrt{3}$+1-1=$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
3.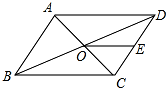 如图,平行四边形ABCD的周长为36,对角线AC、BD相较于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
如图,平行四边形ABCD的周长为36,对角线AC、BD相较于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
 如图,平行四边形ABCD的周长为36,对角线AC、BD相较于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
如图,平行四边形ABCD的周长为36,对角线AC、BD相较于点O,点E是CD的中点,BD=12,则△DOE的周长为( )| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
20.已知两点A(5,6)、B(7,2),先将线段AB向左平移一个单位,再以原点O为位似中心,在第一象限内将其缩小为原来的$\frac{1}{2}$得到线段CD,则点A的对应点C的坐标为( )
| A. | (2,3) | B. | (3,1) | C. | (2,1) | D. | (3,3) |
7.-3的绝对值是( )
| A. | 3 | B. | -$\frac{1}{3}$ | C. | -3 | D. | $\frac{1}{3}$ |
4.某商品经过连续两次降价,销售单价由原来200元降到162元.设平均每次降价的百分率为x,根据题意可列方程为( )
| A. | 200(1-x)2=162 | B. | 200(1+x)2=162 | C. | 162(1+x)2=200 | D. | 162(1-x)2=200 |
 如图,E、F分别是?ABCD的一组对边AD、BC的中点,连接AF、BE相交于点G,EC、DF交于点H
如图,E、F分别是?ABCD的一组对边AD、BC的中点,连接AF、BE相交于点G,EC、DF交于点H