题目内容
19.计算:-22+($\frac{1}{2}$)-1+$\sqrt{(1-tan60°)^{2}}$=$\sqrt{3}$-3.分析 原式第一项利用乘方的意义计算,第二项利用负整数指数幂法则计算,最后一项利用二次根式性质计算即可得到结果.
解答 解:原式=-4+2+$\sqrt{3}$-1=$\sqrt{3}$-3,
故答案为:$\sqrt{3}$-3
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
7.下列各式中,能用平方差公因式分解的是( )
| A. | x2+x | B. | x2+8x+16 | C. | x2+4 | D. | x2-1 |
14.有两根7cm、10cm的木棒,要想以这两根木棒做一个三角形,可以选用第三根木棒的长为( )
| A. | 3cm | B. | 11cm | C. | 20cm | D. | 24cm |
4.有一种美丽的图形,它具有独特的对称美,有无数条对称轴,这种图形是( )
| A. | 等边三角形 | B. | 正方形 | C. | 正六边形 | D. | 圆 |
 如图,△ABC中,AB=8,AC=10,BC=12,D、E分别是AB、AC的中点,则△ADE的周长是15.
如图,△ABC中,AB=8,AC=10,BC=12,D、E分别是AB、AC的中点,则△ADE的周长是15.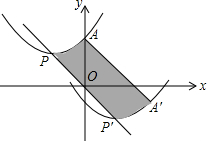 如图,抛物线的顶点为P(-3,3)与y轴交于点A(0,4).若平移该抛物线使其顶点P沿直线移动到点P′(3,-3),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为24.
如图,抛物线的顶点为P(-3,3)与y轴交于点A(0,4).若平移该抛物线使其顶点P沿直线移动到点P′(3,-3),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为24.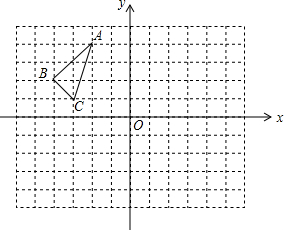 如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图:
如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图: 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).(结果保留根号)
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).(结果保留根号)