题目内容
2．
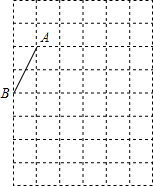如图，在每个小正方形的边长均为1的方格纸中，有线段AB，点A、B均在小正方形的顶点上．（1）在方格纸中画出以AB为一边的直角三角形ABC，点C在小正方形的顶点上，且三角形ABC的面积为$\frac{15}{2}$．
（2）在方格纸中画出以AB为一边的菱形ABDE，点D、E均在小正方形的顶点上，且菱形ABDE的面积为3，连接CE，请直接写出线段CE的长．
分析 （1）利用直角三角形的性质结合勾股定理得出答案；
（2）利用菱形的性质结合勾股定理得出答案．
解答 
解：（1）如图所示：△ABC即为所求；
（2）如图所示：菱形ABDE即为所求，
EC=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$．
点评 此题主要考查了应用设计与作图以及勾股定理以及菱形的性质，正确借助网格得出各边长是解题关键．
练习册系列答案
相关题目
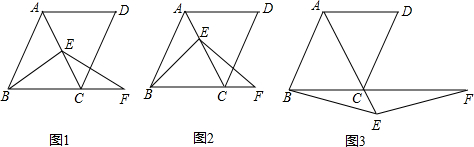
13．已知钝角三角形的三边为2、3、4，该三角形的面积为（ ）
| A． | $\frac{5\sqrt{13}}{4}$ | B． | $\frac{5\sqrt{15}}{4}$ | C． | $\frac{4\sqrt{13}}{5}$ | D． | $\frac{3\sqrt{15}}{4}$ |
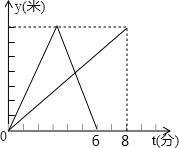小华和爷爷在一环形跑道上匀速跑步，两人在同一起点顺时针出发，两人离起点较近的环形距离y与时间t之间关系如图所示，出发后小华第一次与爷爷相遇的时间为9.6分．