题目内容
6.方程组$\left\{\begin{array}{l}x+y+z=23\\ x-y=1\\ 2x+y-z=20\end{array}\right.$的解是$\left\{\begin{array}{l}{x=\frac{48}{5}}\\{y=\frac{43}{5}}\\{z=\frac{24}{5}}\end{array}\right.$.分析 利用①+②可消去z,再与方程②组成二元一次方程组,再求解即可.
解答 解:
在方程组$\left\{\begin{array}{l}{x+y+z=23①}\\{x-y=1②}\\{2x+y-z=20③}\end{array}\right.$中,
①+③可得:3x+2y=46④,
由②、④组成二元一次方程组$\left\{\begin{array}{l}{x-y=1②}\\{3x+2y=46④}\end{array}\right.$,
由②可得x=y+1,代入④可得:3(y+1)+2y=46,解得y=$\frac{43}{5}$,
∴x=y+1=$\frac{48}{5}$,
把x、y的值代入①可得:$\frac{48}{5}$+$\frac{43}{5}$+z=23,解得z=$\frac{24}{5}$,
∴原方程组的解为$\left\{\begin{array}{l}{x=\frac{48}{5}}\\{y=\frac{43}{5}}\\{z=\frac{24}{5}}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=\frac{48}{5}}\\{y=\frac{43}{5}}\\{z=\frac{24}{5}}\end{array}\right.$.
点评 本题主要考查三元一次方程组的解法,解方程组即“转化”,化高次为低次,注意消元的方法.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
15.下列关于x的方程中,一定有实数根的是( )
| A. | x6+1=0 | B. | $\frac{x}{x-2}$=$\frac{2}{x-2}$ | C. | $\sqrt{x-2}$+3=0 | D. | $\sqrt{2-x}$=x |
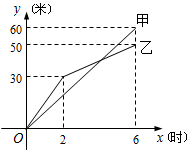 有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.如图是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.如图是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题: