题目内容
12. 已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
已知二次函数y=ax2+bx+2,它的图象经过点(1,2).(1)若该图象与x轴的一个交点为(-1,0).
①求二次函数y=ax2+bx+2的表达式;
②出该二次函数的大致图象,并借助函数图象,求不等式ax2+bx+2≥0的解集;
(2)当a取a1,a2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.
分析 (1)①已知抛物线图象上的两点坐标,且只有两个待定系数,利用待定系数法求解即可;
②画出函数图象,根据图形求出不等式ax2+bx+2≥0的解集;
(2)用a表示出函数的解析式,然后分别将M、N的坐标代入抛物线的解析式中,分别用m、n表示出a1、a2,通过做差可比较出a1、a2的大小.
解答 解: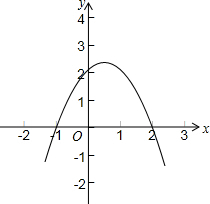 (1)①∵二次函数y=ax2+bx+c经过点(1,2)和(-1,0)
(1)①∵二次函数y=ax2+bx+c经过点(1,2)和(-1,0)
可得$\left\{\begin{array}{l}a+b+2=2\\ a-b+2=0\end{array}\right.$,解得$\left\{\begin{array}{l}a=-1\\ b=1\end{array}\right.$,
即二次函数的表达式为:y=-x2+x+2;
②如图:由图象得:不等式ax2+bx+2≥0的解集为:-1≤x≤2;
(2)∵二次函数与x轴正半轴交与点(m,0)且a=-b
∴${a_1}{m^2}-{a_1}m+2=0$,
即${a_1}=\frac{2}{{m-{m^2}}}$,
同理 ${a_2}{n^2}-{a_2}n+2=0$${a_2}=\frac{2}{{n-{n^2}}}$,
故${a_2}-{a_1}=\frac{2}{{n-{n^2}}}-\frac{2}{{m-{m^2}}}=\frac{2(m-n)(1-m-n)}{mn(1-m)(1-n)}$,
∵n>m>1,
故${a_2}-{a_1}=\frac{2(m-n)(1-m-n)}{mn(1-m)(1-n)}>0$,
∴a1<a2.
点评 本题考查了二次函数的图象与x轴的交点,解析式的确定、函数图象交点坐标的求法以及不等式的应用等知识,综合性较强,属于基础知识的综合考查,难度适中.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
2.我县举行了一次艺术比赛,各年级组的参赛人数如下表所示:
(1)求全体参赛选手年龄的众数,中位数.
(2)王涛说,他所在年龄组的参赛人数占全体参赛人数的24%,你认为王涛是哪个年龄组的选手?请说明理由.
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 5 | 19 | 12 | 14 |
(2)王涛说,他所在年龄组的参赛人数占全体参赛人数的24%,你认为王涛是哪个年龄组的选手?请说明理由.
17.长江是中国第一长河,是世界第三长,中国科学院利用卫星遥感影像测量计算,测出长江长度为6 397 000米.6 397 000这个数字用科学记数法表示为( )
| A. | 6.397×104 | B. | 6.397×105 | C. | 6.397×106 | D. | 6.397×107 |
 如图所示的是某年参加国际教育评估的15个国家学生的数学平均成绩的统计图,则平均成绩大于或等于60的国家个数是12.
如图所示的是某年参加国际教育评估的15个国家学生的数学平均成绩的统计图,则平均成绩大于或等于60的国家个数是12.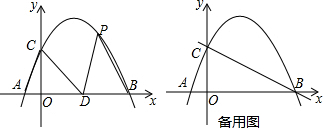

 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=2.5cm,则AB的长为5cm.
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=2.5cm,则AB的长为5cm.