题目内容
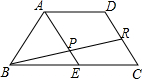 在等腰梯形ABCD中,下底BC是上底AD的两倍,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=( )
在等腰梯形ABCD中,下底BC是上底AD的两倍,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等腰梯形的性质,相似三角形的判定与性质
专题:
分析:先由BC=2AD,BE=EC=
BC,得出BE=EC=AD,根据等腰梯形的性质得到AD∥BC,由一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形,那么EA=CD,EA∥CD.再由三角形中位线定理得出EP为△BCR的中位线,于是EP=
CR,而CR=
CD,那么EP=
CD=
EA,然后根据比例的性质即可求出
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| EP |
| AP |
| 1 |
| 3 |
解答:解:∵BC=2AD,BE=EC=
BC,
∴BE=EC=AD,
∵在等腰梯形ABCD中,AD∥BC,
∴四边形ADCE是平行四边形,
∴EA=CD,EA∥CD.
∵EP∥CR,BE=EC=
BC,
∴EP为△BCR的中位线,
∴EP=
CR,
∵CR=
CD,
∴EP=
CD=
EA,
∴
=
,
∴
=
.
故选A.
| 1 |
| 2 |
∴BE=EC=AD,
∵在等腰梯形ABCD中,AD∥BC,
∴四边形ADCE是平行四边形,
∴EA=CD,EA∥CD.
∵EP∥CR,BE=EC=
| 1 |
| 2 |
∴EP为△BCR的中位线,
∴EP=
| 1 |
| 2 |
∵CR=
| 1 |
| 2 |
∴EP=
| 1 |
| 4 |
| 1 |
| 4 |
∴
| EP |
| EA |
| 1 |
| 4 |
∴
| EP |
| AP |
| 1 |
| 3 |
故选A.
点评:本题考查了等腰梯形的性质,平行四边形的判定与性质,三角形中位线定理,比例的性质,难度适中.得出四边形ADCE是平行四边形,进而求出EA=CD是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
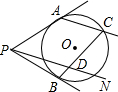 如图,PA与PB切⊙O于A、B,C为优弧
如图,PA与PB切⊙O于A、B,C为优弧
 在△ABC中,∠C=90°,AC=6,BC=8,DE垂直平分AB,求BE的长.
在△ABC中,∠C=90°,AC=6,BC=8,DE垂直平分AB,求BE的长. 如图,点D是△ABC的边BC上的一点,∠B=∠BAD=∠C,∠ADC=72°.
如图,点D是△ABC的边BC上的一点,∠B=∠BAD=∠C,∠ADC=72°. 如图,四边形ABCD中,∠A=60°,则∠1+∠2=
如图,四边形ABCD中,∠A=60°,则∠1+∠2=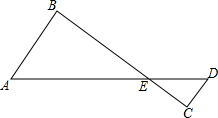 如图,AD、BC相交于点E,且AE=54cm,ED=36cm,CE=30cm,BE=45cm,∠B=78°.
如图,AD、BC相交于点E,且AE=54cm,ED=36cm,CE=30cm,BE=45cm,∠B=78°. 如图,AB,CD相交于点O,OE⊥CD,∠1与∠2叫做
如图,AB,CD相交于点O,OE⊥CD,∠1与∠2叫做