题目内容
18.已知圆内接正三角形面积为$\frac{3}{4}$$\sqrt{3}$cm2,求这个圆的半径.分析 利用三角形半径和边心距的关系,求出半径和边心距及三角形的高的比,根据比例设出边心距,再表示出三角形的高,即可列方程解答.
解答 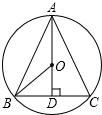 解:如图,
解:如图,
O为△ABC的中心,
AD为△ABC的边BC上的高,
则OD为边心距,
∴∠BAD=30°,
又∵AO=BO,
∴∠ABO=∠BAD=30°,
∴∠OBD=60°-30°=30°,
在Rt△OBD中,
BO=2DO,
即AO=2DO,
∴OD:OA:AD=1:2:3.
在正△ABC中,AD是高,设BD=x,则AD=BD•tan60°=$\sqrt{3}$BD=$\sqrt{3}$x.
∵正三角形ABC面积为$\frac{3\sqrt{3}}{4}$cm2,
∴$\frac{1}{2}$BC•AD=$\frac{3\sqrt{3}}{4}$,
∴$\frac{1}{2}$×2x•$\sqrt{3}$x=$\frac{3\sqrt{3}}{4}$,
∴x=$\frac{\sqrt{3}}{2}$.
即BD=$\frac{\sqrt{3}}{2}$,则AD=$\frac{3}{2}$,
∵OD:OA:AD=1:2:3,
∴AO=1,
∴这个圆的半径为1.
点评 本题考查了圆的内接三角形和外切三角形,根据正三角形的性质和三角函数,求出半径和边心距的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若X=2$\sqrt{2}$+$\sqrt{20}$,Y=3$\sqrt{3}$+$\sqrt{7}$,Z=$\sqrt{6}$+2$\sqrt{7}$,则( )
| A. | X最小 | B. | Y最小 | C. | Z最小 | D. | X、Y、Z一样大 |
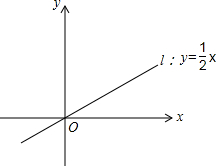 如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$.
如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$. 已知:如图数轴上两点A、B所别应的分别为-3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
已知:如图数轴上两点A、B所别应的分别为-3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒. 跳绳时,绳甩到最高处时的形状是抛物线.以点O为原点建立如图所示的平面直角坐标系,此时抛物线的解析式为y=-0.1x2+0.6x+0.9.
跳绳时,绳甩到最高处时的形状是抛物线.以点O为原点建立如图所示的平面直角坐标系,此时抛物线的解析式为y=-0.1x2+0.6x+0.9.