题目内容
7.一个正多边形的边长是半径的$\sqrt{2}$倍,则这个正多边形的边数为4.分析 根据题意得出AB2=OA2+OB2,由勾股定理的逆定理得出∠AOB=90°,即可求出正多边形的边数.
解答 解:如图所示:
AB为正多边形的一条边长,连接OA、OB,
根据题意得:AB=$\sqrt{2}$OA,
∴AB2=2OA2=OA2+OB2,
∴△AOB是直角三角形,∠AOB=90°,
∵$\frac{360°}{90°}$=4,
∴这个正多边形的边数为4;
故答案为:4.
点评 本题考查正多边形的性质、勾股定理的逆定理;根据题意和勾股定理的逆定理证明△AOB是直角三角形是解决问题的关键.

练习册系列答案
相关题目
15.一种商品按销售量分三部分制定销售单价.如下表:
(1)若买100件花250元,买300件花690元.
(2)小明买这种商品花了n元.解决下列问题:
①小明买了这种商品多少件(用n的式子表示);
②如果小明买这种商品的件数恰好是0.45n件,求n的大小.
| 销售量 | 单价 |
| 不超过100件的部分 | 2.5元/件 |
| 超过100件不超过300件的部分 | 2.2元/件 |
| 超过300件的部分 | 2元/件 |
(2)小明买这种商品花了n元.解决下列问题:
①小明买了这种商品多少件(用n的式子表示);
②如果小明买这种商品的件数恰好是0.45n件,求n的大小.
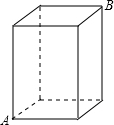 如图是一个长方体,它的底面是一个边长为2cm的正方形,高为3cm,一只蚂蚁要从顶点A爬行到顶点B,则这只蚂蚁爬行的最短路程为5cm.
如图是一个长方体,它的底面是一个边长为2cm的正方形,高为3cm,一只蚂蚁要从顶点A爬行到顶点B,则这只蚂蚁爬行的最短路程为5cm.