题目内容
 如图,已知直线l⊥x轴于点D,点B(-1,y)为直线l上的动点,点C(x,0)为x轴上的动点,且-1<x<4,若点A(4,5),AC⊥BC,则y与x之间的函数关系式
如图,已知直线l⊥x轴于点D,点B(-1,y)为直线l上的动点,点C(x,0)为x轴上的动点,且-1<x<4,若点A(4,5),AC⊥BC,则y与x之间的函数关系式考点:相似三角形的判定与性质,坐标与图形性质
专题:
分析:求出BD=y,CD=1+x,CM=4-x,AM=5,过A作AM⊥x轴于M,证出△BDC∽△CMA,推出
=
求出即可.
| y |
| 4-x |
| 1+x |
| 5 |
解答:解:
∵A(4,5),B(-1,y),C(x,0),
∴BD=y,CD=1+x,CM=4-x,AM=5,
过A作AM⊥x轴于M,
∵AC⊥BC,直线l⊥x轴,
∴∠BDC=∠BCA=∠AMC=90°,
∴∠DBC+∠BCD=90°,∠BCD+∠ACM=90°,
∴∠DBC=∠ACM,
∴△BDC∽△CMA,
∴
=
∴y=-
x2+
x+
,
故答案为:y=-
x2+
x+
.

∵A(4,5),B(-1,y),C(x,0),
∴BD=y,CD=1+x,CM=4-x,AM=5,
过A作AM⊥x轴于M,
∵AC⊥BC,直线l⊥x轴,
∴∠BDC=∠BCA=∠AMC=90°,
∴∠DBC+∠BCD=90°,∠BCD+∠ACM=90°,
∴∠DBC=∠ACM,
∴△BDC∽△CMA,
∴
| y |
| 4-x |
| 1+x |
| 5 |
∴y=-
| 1 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
故答案为:y=-
| 1 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
点评:本题考查了坐标与图形性质,相似三角形的性质和判定,解此题的关键是求出两三角形相似,题目比较好,难度适中.

练习册系列答案
相关题目
 如图,A、B、C三点在⊙O上,且∠ABO=50°,则∠ACB等于( )
如图,A、B、C三点在⊙O上,且∠ABO=50°,则∠ACB等于( )| A、100° | B、80° |
| C、50° | D、40° |
下列说法正确的是( )
| A、三角形的内心是这个三角形三条边中垂线的交点 |
| B、矩形的对角线相等的逆命题是真命题 |
| C、一组数据2、9、7、5、4、8、5、3的中位数是5 |
| D、正六边形的外角和是720度 |
 如图,在△ABC中,已知AB=AC=6,BC=8,且∠B=∠DEF(足够大)与△ABC重叠在一起,即∠B与∠DEF重合,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动(不与点B,C重合),且DE始终经过点A,EF与AC交于点M.
如图,在△ABC中,已知AB=AC=6,BC=8,且∠B=∠DEF(足够大)与△ABC重叠在一起,即∠B与∠DEF重合,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动(不与点B,C重合),且DE始终经过点A,EF与AC交于点M.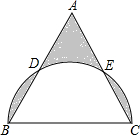 如图,在边长为2的正三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E.则图中阴影部分的面积是
如图,在边长为2的正三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E.则图中阴影部分的面积是 某公司计划在一座圆锥形土丘上铺满草皮,土丘高50米,坡度i=1:
某公司计划在一座圆锥形土丘上铺满草皮,土丘高50米,坡度i=1: