题目内容
3.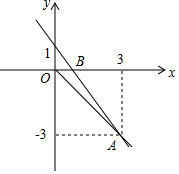 函数y=kx+1的图象经过点A(3,-3),且与x轴相交于B点,O为坐标原点.
函数y=kx+1的图象经过点A(3,-3),且与x轴相交于B点,O为坐标原点.(1)说明y随x的变化情况.
(2)求B点的坐标.
(3)求三角形OAB的面积.
分析 (1)把点A(3,-3)代入y=kx+1,求得k,根据一次函数的性质即可求得y随x的变化情况;
(2)令y=0,求得x的值,即可求得B的坐标;
(3)根据三角形面积公式即可求得.
解答 解:(1)∵函数y=kx+1的图象经过点A(3,-3),
∴-3=3k+1,
∴k=-$\frac{4}{3}$,
∴y随x的增大而减小;
(2)令y=0,则-$\frac{4}{3}$x+1=0,
解得x=$\frac{3}{4}$,
∴B($\frac{3}{4}$,0);
(3)三角形OAB的面积=$\frac{1}{2}$×$\frac{4}{3}$×3=2.
点评 本题考查了待定系数法求一次函数的解析式、一次函数图象上点的坐标特征以及根据图象与坐标轴的交点求直线与两坐标轴围成三角形的面积,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列计算结果为正数的是( )
| A. | -76×5 | B. | (1-7)6×5 | C. | 1-76×5 | D. | (1-76)×5 |
11.从重庆北开往北京的特快车,途中要停靠四个站点,如果任意两个间的票价不同,那么不同票价有( )种.
| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
15.若5x2-3xy+y2与一个多项式的和是3xy-x2,则这个多项式是( )
| A. | 6x2-3xy+y2 | B. | -6x2+6xy-y2 | C. | 4x2+y2 | D. | -6x+y2 |