Question

8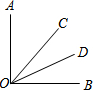．如图，∠AOC=40°，OD平分∠BOC．
（1）如果∠AOB=90°，求∠AOD的度数．
（2）如果∠AOB的度数为x（40＜x＜180），用含x的代数式表示∠AOD的度数．
（3）∠AOB的度数是多少时，∠AOD=90°？

Answer 1

分析 （1）先利用互余得到∠BOC=50°，再根据角平分线定义得∠BOD=$\frac{1}{2}$∠BOC=25°，然后利用∠AOD=∠AOB-∠BOD进行计算即可；
（2）与（1）一样，先得到∠BOC=∠AOB-∠AOC，再根据角平分线定义得∠BOD=$\frac{1}{2}$∠BOC=$\frac{1}{2}$（∠AOB-∠AOC），于是得到∠AOD=$\frac{1}{2}$（∠AOB+∠AOC）；
（3）利用（2）的结论得到$\frac{1}{2}$（∠AOB+40°）=90°，然后解方程求出∠AOB的度数．

解答 解：（1）∵∠AOB=90°，∠AOC=40°，
∴∠BOC=90°-40°=50°，
∵OD平分∠BOC，
∴∠BOD=$\frac{1}{2}$∠BOC=25°，
∴∠AOD=∠AOB-∠BOD=90°-25°=65°；
（2）∠BOC=∠AOB-∠AOC，
∵OD平分∠BOC，
∴∠BOD=$\frac{1}{2}$∠BOC=$\frac{1}{2}$（∠AOB-∠AOC），
∴∠AOD=∠AOB-$\frac{1}{2}$（∠AOB-∠AOC）=$\frac{1}{2}$（∠AOB+∠AOC）；
（3）∵∠AOD=$\frac{1}{2}$（∠AOB+∠AOC）；
∴$\frac{1}{2}$（∠AOB+40°）=90°，
∴∠AOB=140°，
即）∠AOB的度数是140°时，∠AOD=90°．

点评 本题考查了角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．