题目内容
15. 如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.
如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.(1)直接写出点A、B的坐标:A(0,1),B(-1,-1);
(2)请在图中确定点C(1,-2)的位置并连接AC、BC,则△ABC是等腰直角三角形(判断其形状);
(3)在现在的网格中(包括网格的边界)存在一点P,点P的横纵坐标为整数,连接PA、PB后得到△PAB为等腰三角形,则满足条件的点P有8个.
分析 (1)根据平面直角坐标系可直接写出A、B的坐标;
(2)画出图形,利用勾股定理计算出AB2、CB2、AC2,再利用逆定理证明△ACB是等腰直角三角形;
(3)分别以A、B为圆心,AB长为半径画圆可得P的位置及个数.
解答 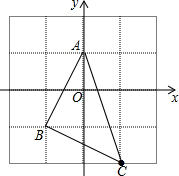 解:(1)根据平面直角坐标系可得A(0,1),B(-1,-1),
解:(1)根据平面直角坐标系可得A(0,1),B(-1,-1),
故答案为:0;1;-1;-1;
(2)∵AB2=12+22=5,CB2=12+22=5,AC2=12+32=10,
∴AB2+BC2=AC2,
∴△ACB是等腰直角三角形,
故答案为:等腰直角;
(3)如图所示: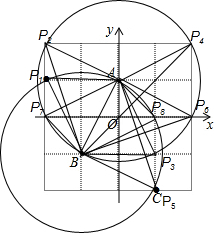 ,
,
满足条件的点P有8个,
故答案为:8.
点评 此题主要考查了等腰三角形的判定,以及平面直角坐标系中点的坐标,勾股定理和逆定理,关键是掌握两边相等的三角形是等腰三角形.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
5. 已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
 已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
3.小明利用二次函数的图象估计方程x2-2x-2=0的近似解,如表是小明探究过程中的一些计算数据.根据表中数据可知,方程x2-2x-2=0必有一个实数根在( )
| x | 1.5 | 2 | 2.5 | 3 | 3.5 |
| x2-2x-2 | -2.75 | -2 | -0.75 | 1 | 3.25 |
| A. | 1.5和2之间 | B. | 2和2.5之间 | C. | 2.5和3之间 | D. | 3和3.5之间 |
7.若3x3yn-1与-xm+1y2是同类项,则m-n的值为( )
| A. | -1 | B. | 0 | C. | 2 | D. | 3 |
4.下列计算正确的是( )
| A. | 3a2-a2=2 | B. | 2m2+m2=3m4 | C. | 3m2-4m2=-m2 | D. | -ab2+2ab2=-2ab2 |

 如图,一轴对称图形画出它的一半,请你以图中虚线为对称轴画出它的另一半.
如图,一轴对称图形画出它的一半,请你以图中虚线为对称轴画出它的另一半. 如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.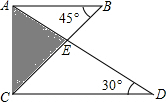 将一副三角尺按如图所示的方式叠放在一起,边AD与BC相交于点E,则$\frac{BE}{EC}$的值等于$\frac{{\sqrt{3}}}{3}$.
将一副三角尺按如图所示的方式叠放在一起,边AD与BC相交于点E,则$\frac{BE}{EC}$的值等于$\frac{{\sqrt{3}}}{3}$.