题目内容
5.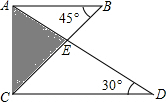 将一副三角尺按如图所示的方式叠放在一起,边AD与BC相交于点E,则$\frac{BE}{EC}$的值等于$\frac{{\sqrt{3}}}{3}$.
将一副三角尺按如图所示的方式叠放在一起,边AD与BC相交于点E,则$\frac{BE}{EC}$的值等于$\frac{{\sqrt{3}}}{3}$.
分析 设AB=AC=1,根据勾股定理求出BC,求出AD=2AC=2,根据勾股定理求出DC,求出AB∥CD,得出相似△AEB∽△DEC,得出比例式,代入求出即可.
解答 解:设AB=AC=1,由勾股定理得:BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∵在Rt△ACD中,∠ACD=90°,AC=1,∠D=30°,
∴AD=2AC=2,由勾股定理得:DC=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵∠BAC+∠CD=90°+90°=180°,
∴AB∥CD,
∴△AEB∽△DEC,
∴$\frac{AB}{CD}$=$\frac{BE}{CE}$,
∴$\frac{BE}{EC}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了相似三角形的判定和性质,含30°角的直角三角形性质,平行线的判定,勾股定理的应用,能得出相似三角形和求出AB、BC、CD的长是解此题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
16.在下列各项中,可以用平方差公式计算的是( )
| A. | (2a+3b)(3a-2b) | B. | (a+b)(-a-b) | C. | (-m+n)(m-n) | D. | ($\frac{1}{2}$a+b)(b-$\frac{1}{2}$a) |
20.校运动会上甲、乙、丙、丁四名选手参加100米决赛,赛场有1、2、3、4条跑道.如果选手以随机抽签的方式决定各自的跑道,则甲抽到1号跑道,乙抽到2号跑道的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
17.下列方程中是一元一次方程的是( )
| A. | x+3=3-x | B. | x+3=y+2 | C. | $\frac{1}{x}$=1 | D. | x2-1=0 |
 如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.
如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系. 如图,等边△ABC周长是12,AD是∠BAC的平分线,则BD=2.
如图,等边△ABC周长是12,AD是∠BAC的平分线,则BD=2. 在边长为1的小正方形网格中,△ABC的顶点均在格点上,
在边长为1的小正方形网格中,△ABC的顶点均在格点上,