题目内容
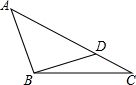如图，已知：△ABC中，BC=6．（1）如果AC=9，边AC上是否存在一点D，使△ABC∽△BDC？如果存在，如果存在，请求出CD的长度．
（2）如果BD=4，求AB：DC的值．
考点：相似三角形的判定与性质
专题：常规题型
分析：（1）由相似三角形的对应边成比例可直接得出DC的长度；
（2）根据相似三角形对应边比例相等的性质即可解题．
（2）根据相似三角形对应边比例相等的性质即可解题．
解答：解：（1）存在点D．
∵△ABC∽△BDC，
∴
=
，即
=
，
解得：CD=4．
即CD的长度为4．
（2）∵△ABC∽△BDC，
∴
=
=
，
∴AB=6，CD=4，
∴AB：DC=3：2．
∵△ABC∽△BDC，
∴
| AC |
| BC |
| BC |
| CD |
| 9 |
| 6 |
| 6 |
| CD |
解得：CD=4．
即CD的长度为4．
（2）∵△ABC∽△BDC，
∴
| AB |
| BD |
| AC |
| BC |
| BC |
| CD |
∴AB=6，CD=4，
∴AB：DC=3：2．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，本题中求证△ABC∽△BDC是解题的关键．
练习册系列答案
相关题目
如图，在公路L的一侧有A、B两个村庄，A、B到公路的距离AE和BD分别为300米和480米，且DE为1300米，现要在公路边建一供水站C，向两村庄供水，且使水管最短．
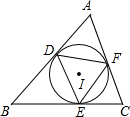已知⊙I是锐角△ABC的内切圆，点D、E、F是三个切点，则△DEF的形状是（ ）| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
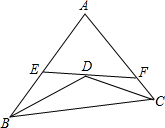如图，BD，CD分别平分∠ABC，∠ACB，过点D作直线分别交AB，AC于点E，F，若AE=AF，BE=4，CF=2，则EF的长为（ ）
